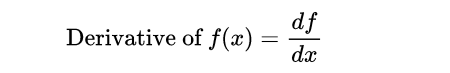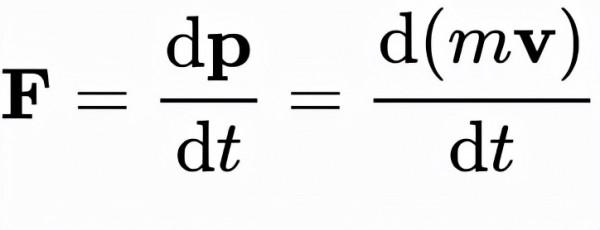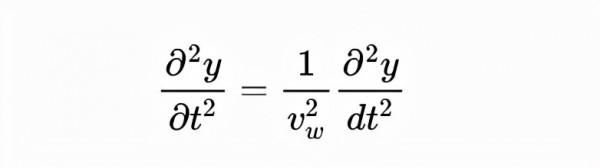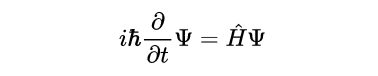我們都或多或少地接觸過導數。網際網路上有很多關於導數的定義。它是一個函式的圖形的切線的斜率。或者，它是 "瞬時變化率"。儘管上述定義在技術上並無不妥，但它們並沒有抓住導數的本質。

讓我們退一步來說。在數學中，我們用數學函式來模擬一個物理量（甚至非物理量）的行為如何取決於另一個量。例如，考慮下面這個函式。

• 兩個質量之間的引力

函式F計算了兩個質量在距離r處的引力。我們說力F是因變數，而 r，即距離，是自變數。r 的值決定了 F 的值。引力是距離的函式，我們寫成F=F(r)。

我們可以想出一個更簡單的函式。比方說f(x)=x²。這個函式可以代表一個力或我們選擇的任何量。

一個函式是一個依賴於另一個量的量。這種依賴關係的確切性質是由函式的公式描述的。然而，公式中沒有描述的是這種依賴關係的“敏感度”。考慮一下我們之前提到的函式F=F(r)。儘管我們有引力的公式，但我們不知道引力對自變數距離的變化有多大的反應。也就是說，如果我們改變了距離，力會改變多少？這就是衍生出導數概念的問題。

函式f=f(x)的導數告訴我們，當我們把引數x改變一些時，函式f(x)的變化有多快。如果 "df "代表函式f(x)的微小變化，"dx "代表自變數 "x "的微小變化，那麼導數就是比例因子。

應用

很難想象沒有導數的數學和物理學。我們現在將看到這個概念的一些應用，以及為什麼使用它不僅是必要的，而且是合乎邏輯的。

• 艾薩克-牛頓和戈特弗裡德-威廉-萊布尼茨獨立發展了無窮小微積分理論。

數學

導數在數學中的一個直接應用是當我們試圖判斷一個函式是（單調）增還是減。牢記導數的定義，要想得出這個想法並不難。如果一個函式f(x)的導數是正的，那麼這個函式將是單調增的，如果是負的，它就是單調減的。在這篇文章中，我所關心的不是精確的數學，而是背後的直覺。想一下，如果我們把 "x "改變一個很小的量 "dx"，而f(x)改變的量 "df "是正的，這意味著f正在變大。換句話說，這個函式在增加。同樣的說法也適用於遞減函式。

當我們試圖確定一個函式的最小值和最大值時，導數也會很有用。讓我們再想一下，在一個函式達到其最大值的地方，導數必須是什麼？當然，它必須是零。只有當 "df "為零時，函式才會出現最小值或最大值。

物理學

導數在物理學中也發揮著重要的作用。什麼是速度？？我們可以說它是一個物體行進的距離除以到達那裡的時間，但這隻能告訴我們平均速度。我們感興趣的是如何定義瞬時速度，即一個物體在每個時間點上的速度和方向。

在物理學中，對速度有一個非常自然的定義。它是一個物體的位置的導數! 它是一個物體的位置在一個微小的時間變化中的微小變化的分數。那麼什麼是加速度呢？它是速度的導數! 透過這個例子，我們可以看到導數的概念是多麼簡單而又強大。

• 物理學中的位置、速度和加速度

我們研究一個物理量的變化是如何影響依賴於它的其他量的。這就是為什麼在每個物理學領域，從經典力學和電動力學到量子力學和相對論，核心方程都包含導數的原因。以下是一些例子。

• 經典力學中的牛頓第二定律

• 波浪方程

• 量子力學中的薛定諤方程

上述方程是所有物理學中最基本的一些方程。在物理學中，我們很少關注精確的數量。物理學和我們周圍的世界一樣，都是關於變化的。而只有透過導數的概念，我們才能開始理解這個複雜的世界和它所帶來的各種現象。