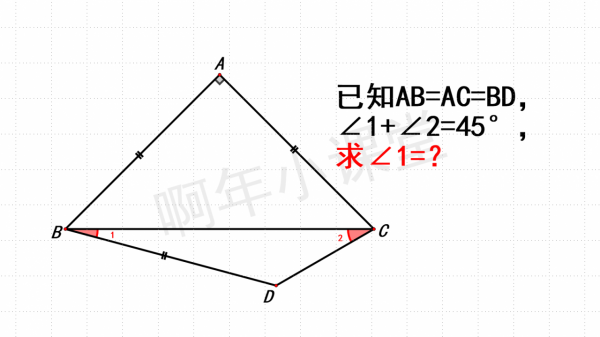
已知AB=AC=BD,∠1+∠2=45°,求∠1=?
這題怎麼做呢?
觀察題目資訊,45°非常特殊。∠1+∠2=45°,可得∠D=135°,以及∠D的外角為45°。
45°在直角三角形中非常有用,我們不妨構造出一個直角三角形。
有2種思路。
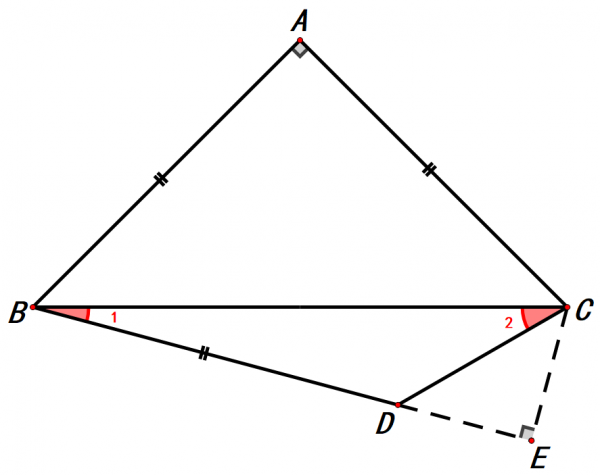
1.延長BD,過點C作BD延長線的垂線
2.延長CD,過點B作CD延長線的垂線
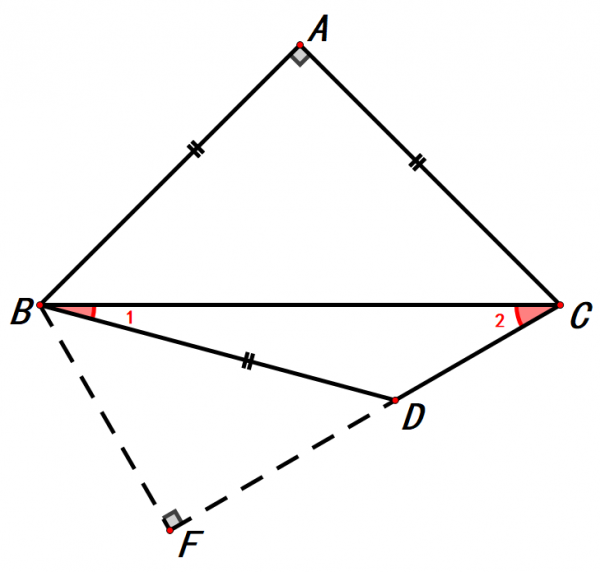
以上2種作輔助線的思路,對於這道題來說,方法2會好一些。
我們看到方法2的圖。圖中有2個等腰直角三角形,三角形ABC和三角形BDF。而AB=AC=BD,三角形ABC和三角形BDF的邊是不是存在一定的數量關係。我們能否透過邊的數量關係求出∠1或者∠2的度數。
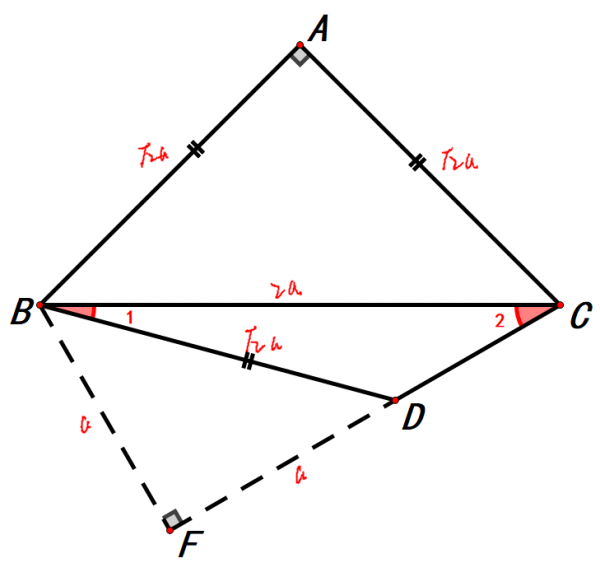
假設BD長度為a,DF=a,則BD=√2a,AB=AC=BD=√2a,BC=2a。
大家有沒有發現在直角三角形BCF中,直角邊BF的長度為斜邊BC的一半,有這樣一個數量關係的直角三角形是30°、60°直角三角形。直角邊BF所對的角為30°,即∠2=30°,題目條件有∠1+∠2=45°,由此可得∠1=15°。
這道題的解題方法非常多,大家還有其他的好方法嗎?歡迎在評論區留言~