在藝術家試圖用影象的方式在平面上創造空間和三維形式的錯覺時,射影幾何學(Projective geometry)就誕生了。數學上,射影幾何是研究關於射影變換不變下的幾何性質的專門學問。而它在物理上還展現了特別的意義,從狹義相對論用四維時空所描述開始,到晶體結構以及通向量子引力的路徑上等等,這項在19世紀蓬勃發展的學問至今仍煥發著生機。
《時空投影:第四維在科學和現代藝術中的表達》作者託尼·羅賓是當代著名藝術家,四維幾何計算機視覺化的先驅。他在探索藝術上起源於畢加索的立體主義(Cubism)的不同四維模型表達時,也探究了它們在現代數學思想和物理學的應用,將藝術與藝術史、數學與科學融合在一起。本文即討論彭羅斯提出的扭量理論中包含的射影幾何思想,彭羅斯將其與複數聯絡在一起構建出時空本身,並由此發展出一系列的強大的數學工具。來自藝術家的視角將幫助我們理解這門深奧的理論。
“這是一部修正主義數學史,也是一部修正主義藝術史。”本文選自《時空投影:第四維在科學和現代藝術中的表達》第7章,有刪減,小標題為編者所加。前往“返樸”公眾號,點選文末“閱讀原文”可購買此書。點選“在看”並發表您的感想至留言區,截至2021年11月7日中午12點,我們會選出2條留言,每人贈書1本。
撰文 | 託尼·羅賓
翻譯 | 潘可慧 潘濤
校譯 | 潘濤
空間真的是由無量綱點(dimensionless points)組成的嗎?高中數學和常識說它是,但有另一種數學和常識說之前就錯了。為了說明常識的謬誤,愛因斯坦舉了一個椅子被推到舞臺上的例子。常識認為,推力移動椅子,因為當推力停止時,椅子就停止。原因和結果再清楚不過了。但是,你可以猛推一把椅子,這樣它就會在沒有人推的時候繼續移動。這個小小的反例,給常識帶來了難題。對此反例的長期考慮最終導致了對摩擦力的研究(牛頓第一定律指出,運動中的物體繼續運動直到停止),這導致了對行星圍繞太陽的運動的理解。物理學家羅傑· 彭羅斯也以類似的方式關注了直線有時是點這一表觀佯謬。圍繞這一佯謬的研究,他得出了一個全新的空間概念,並有希望將物理學各個獨立的、看似不可調和的分支統一起來。
光 錐
在開始考察彭羅斯佯謬(Penrose’s paradox)前,請先考慮光錐(light cone),它是所有聚集在時間和空間點上的光的一部分。此外,在當前時刻,光的閃光從一個特定的位置擴充套件,而作為向外傳播的光線的前緣的球面形成了光錐的上半部。因為很難想象四維圖形,所以慣例是把光錐畫成雙尖紙帽,其中的圓圈代表光的球面,兩條邊代表光的時間流逝的歷史。對於許多討論點,在較低維度情況下的推理與在較高維度的情況下的推理是相同的,且繪圖更容易。
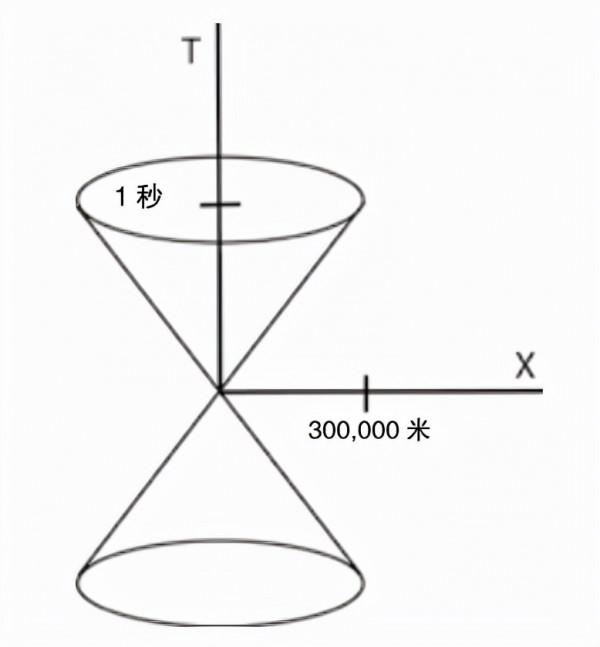
“夾點”表示空間中某一特定位置的當前時刻。沿著光錐的垂直時間軸傳播,就是在時間流逝時停留在原地;沿水平軸傳播是隨時隨地,以無限的速度運動。這些軸可以校準,這樣垂直軸上的一個滴答等於 1 秒,而水平軸上的一個滴答等於 300,000 米。透過這種校準,在 45 度對角線上運動就是以光速傳播(圖1)。
圖1 光錐。對軸進行校準,使光速以 45 度線表示
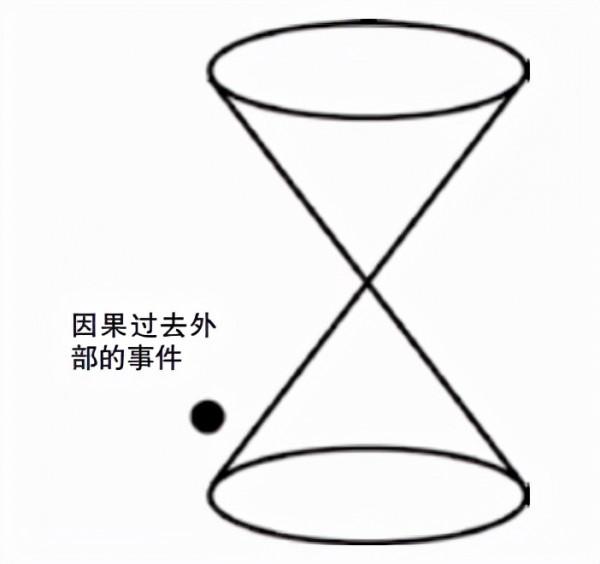
因為面朝下的光錐是由所有在特定時刻特定位置聚集在一起的光線組成的,所以觀察者在這個夾點所能知道的就是錐內的資訊。在內部,慢於光速的光線就可以到達觀察者;在外部,光線或資訊的傳播速度必須比光速更快才能到達觀察者,這是不可能的。因此,面朝下的光錐代表因果過去。同理,面朝上的光錐從那時起就描述了在那個地方因果未來的所有可能性。光錐表面則代表恰好以光速行進的光線或資訊(圖 2)。
圖2 面朝下的光錐描繪了因果過去。因果過去以外的事件,不會影響那個夾點(即在那個位置的當前時刻)
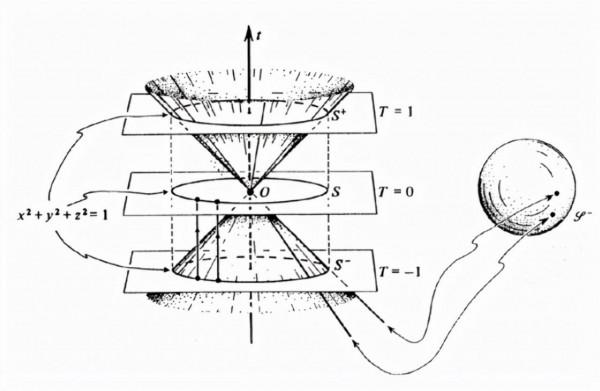
圖3 彭羅斯畫的光錐。光錐表面上的直線代表以光速行進的路徑。相對論表明,對於旅行說,這些路徑的長度為零;它們是零射線,也可以用球面上的點來表示。
要使這一論證具體化,需考慮一個在恆星 4.3 光年之外的核爆炸中產生的光子,它被眼睛吸收並轉化為化學能時,就結束了它的存在。其路徑長度約為 4.06×10^13米。但是,如果某人以非常高的速度行駛,那麼這條路可能只有原來的一半長;在 95% 的光速下,這條路只有原來距離的 30%。
考慮那個著名的雙生子例子,如果一個人乘坐宇宙飛船,以接近光的速度旅行,而另一個人待在地球上,這對雙胞胎的年齡就不一樣了。或者,對於那些不那麼喜歡假設的物理謎語的人來說,要考慮粒子加速器,當物質加速到接近光速時,放射性物質樣本的半衰期實際上會根據靜止時鐘(以及與其他物質相比)減慢。狹義相對論方程所描述的扭曲是有物理實在(physical reality)的,光錐圖必須解釋這一事實。
彭羅斯的替代光錐也提供了誤導的資訊,因為它沒有顯示所有作為點的光線的球面從現在開始縮小或向外生長,就像產生閃光時的情形。包括零在內的各種長度的光線佯謬是由描述它們的空間模型產生的,如果它們被認為是空間中的直線(line in space),模型中的問題就不可避免。彭羅斯的創造性飛躍,乃是意識到還有另一個幾何物件可以模擬光線:射影直線(projective line)可以容納光線的所有長度。(為了保持術語清晰,我將射影幾何中的線稱為“射影直線”,而在其他幾何學中稱之為“空間中的直線”,這是強調射影直線與背景無關的區別。)
從表面上看,射影直線看起來像是空間中的直線,但它卻截然不同,更加豐富。在射影幾何中,存在著直線和點的基本對偶論;凡是談論其中一個,就可以談論另一個。射影點用比率(齊次座標)表示,高維空間中所有滿足這一比例的點都被認為是同一點。一旦這種想象飛躍發生,射影直線就越來越準確地描述了光線。射影直線具有一系列有序的點,但是——類似於光線——它們沒有確定的長度。就這一點而言,射影直線上某一範圍內的點可以透過多個射影變換合法地重新排列,那些投影將一條直線投影回自身,這對於空間中的直線上的點來說則不可想象。19 世紀射影幾何的成就是逐漸將射影幾何從笛卡兒 x, y 網格中移除,並跟蹤因不同投影而變化的測量值時,在圖形中保持不變的情況。因此,並不存在網格是射影直線(即光線)的專有定義。
沒有潛在的空間網格的事件空間的前景,對物理學家來說是很有吸引力的。一段時間以來他們一直對物理學的戲劇應該在一個預先確定的空間(不管它如何彎曲或扭曲)舞臺上發揮出來的想法感到不爽。根據廣義相對論,空間是物質的創生。根據粒子物理學,物質在空間之外產生,是從時空的虛粒子(幾乎不可能有任何物質的單位)中冒出來的。如今弦理論提出,物質最終由一維實體組成,與任何三維物質單位相比,一維實體對純幾何的親和力要大得多。圈量子引力(loop quantum gravity)比其他形式的弦理論有價值,它的發明者之一李·斯莫林(Lee Smolin)說,這主要是因為“我們真的可以以一種背景獨立的方式來看待空間和時間,把它們看作一個關係網”(Smolin 2001,179 頁)。對於彭羅斯來說,這些關係網的單位由射影直線構建:“我們把時空認為是從屬的概念,而把扭量空間——原先是光線空間——認為是更基本空間。”(Hawking and Penrose 1996,110 頁)“通常的時空概念……是由扭量基本成分構造出來的。” (Penrose 2004,963頁)
扭量空間
彭羅斯經常寫道,想象一位觀看夜空的觀者,恆星的宇宙就像一個球體(被稱為“天球”或者“天圖”),觀者在其中心。另一位站在離第一位觀者一段距離的觀者,也看到了一個天球。通常情況下,這兩個球體可以簡單地透過旋轉一個球體使之與另一個球體重合在一起。然而,如果第二個觀者以接近光速行進,這種方法將無法奏效;球體中存在光的畸變,簡單的旋轉不會產生重合。例如,如果第二個觀者直接從靜止的第一個觀者身邊經過,但正以很大的速度向北極星移動,那麼天球上的恆星就會被擠壓到北極區;如果第二個觀者經過第一個觀者的一側,天球上的恆星將被旋轉到一邊,然後擠壓到北方。當然,運用洛倫茲變換會從另一組重新計算一組恆星位置,但是彭羅斯注意到一組更簡單的變換,即莫比烏斯變換(與莫比烏斯帶沒有關係)也會獲得成功。
要使莫比烏斯變換起作用,天球上的位置必須用複數重新編號:形為a +b i 的數字,其中 i 是虛數
。複數通常表示在平面上,其中第一個數
(實部)是在水平軸上的位置,第二個數(虛部)是在垂直軸上的位置,完全複數是用這兩個軸作為地圖座標定義的平面上的位置。這整個二維平面,代表了一組相關的復點(complexpoints),可以被認為是一條復直線(complex line)。射影直線的行為就好像它們是封閉的,因此經常被建模成圓:左無窮大和右無窮大是一樣的。“所選擇的(射影幾何的)公理非常普遍,允許座標屬於任何場:不是我們可以使用有理數的實數,而是複數。”(Coxeter 1961,231 頁)因此,射影直線需要不僅是一條實點直線,還可以是一條由複數組成的直線。若它既是複數又是射影,則直線就只有一個無窮遠點。這條複線,被建模成只有一個無窮遠點的平面,捲成一個球,稱為黎曼球面。
對於莫比烏斯變換,天球被對映到這個數學球面上。若使用極座標(從球面中心的角度匯出)代替經度和緯度座標,則計算進一步簡化。這種對複數和極座標的改變,結果是一個意想不到的好處。不僅洛倫茲變換的計算更容易進行,彭羅斯說的廣義相對論中的計算也更容易進行。此外,射影空間中的複數是量子物理工作的首選數學系統;至少這兩個不同的物理學分支現在可以使用同一種數學語言。
彭羅斯指出,“在基本的扭量對應中,(閔可夫斯基)時空中的光線在(射影)扭量空間中用點來代表,而時空點則表示為黎曼球面”(Hawking and Penrose 1996,111 頁)。當用齊次座標表示時,空間中的直線就變成了點。當做出射影和復時,點變成復射影直線,即黎曼球面。彭羅斯將光線射影模型的相關性與複數的便利性結合起來,構造了復射影三維空間,即扭量空間(twistor space)的定義(圖4)。扭量不是無質量粒子,不像向量是無質量粒子,但扭量是對無質量粒子可能性的描述,因此是對空間的描述(圖 5)。在許多著作和講座中,他對這些元素之間的有機聯絡感到驚訝:天球的狹義相對論洛倫茲變換也是莫比烏斯變換;莫比烏斯變換假定黎曼球面及其內含的復射影幾何;光線最好模擬成射影直線。
圖4 射影直線,畫成圓圈,把(過去的)天球和(未來的)天球連線起來
圖5 彭羅斯畫的扭量,一個巢狀的一系列墨水圓圈,填充了所有的三維空間
我找到了我的空間!
射影幾何學和複數的結合還有進一步的協同作用,這是一個凝聚在一起的整體,遠遠大於其各部分看似無害的總和。描述無質量粒子自旋的此種自然方式,就是這些令人欣喜的結果之一。
觀者總是位於天球光線的中心,因為光線在當前時刻聚集在一個特定的位置上,組成觀者的天圖(sky map)。這些光線,若延續到未來,則構成未來一半的光錐,即觀者的反天圖(anti-sky map)。對於光線本身,這兩幅天圖被“視為等同”,意思是它們被合(即“膠合”)在一起因為光線的長度為零。彭羅斯謹慎地說,過去光錐和未來光錐的這個緊化(一個數學術語,指“系統的完成”)只是一個數學上的“方便”,但是一個有資訊的“方便”。光線穿過夾點時,它們的位置在光錐的上半部分被反轉。緊化,就相當於在光線中加一個扭曲(圖 6)。
圖6 當過去天圖與未來天圖膠合時,緊化就會發生。當連線對應諸點的諸線長度為零時,此種膠合是不可避免的。
另一種將光錐緊化的方法,是在閔可夫斯基空間(Minkowski space)中新增一個無窮遠光錐(圖 7)。新增一個無窮遠元素,是射影幾何封閉一個空間的既定技巧。這種緊化的結果,構造了復射影三維空間。彭羅斯意識到,由閉環組成的緊化光錐是三維球面(球面的四維類似物)的霍普夫纖顫(一組連結的圓)。這是一個久已為人所知的數學事實,即在三維球上的某些平行路徑隨著它們的推進而扭曲。彭羅斯認為,這一幾何事實必須解釋無質量粒子自旋的起源,儘管所有的細節還沒有搞清楚。為了界定光線扭轉的方向,光線的描繪必須有一個附加的結構,而這是透過新增旗子來實現的:把光線看作旗杆,把旗子看作附在旗杆上的剛性訊號旗(圖8 )。(旋量,即隨它們推進而旋轉的向量,就是這樣被描述的,而扭量則以旋量數學為基礎。)現在可以跟蹤零射線(零長度的光線)的扭曲,並將其看作緊化的必然結果,緊化本身就是在其自身參考系中具有零長度,從而成為一個射影實體的光線的必然結果。
圖7 放置一個無窮遠光錐,會使零射線變成圓。放置一個無窮遠光錐,也會使空間緊化。
圖8 零射線的切線和垂線從過去傳遞到未來時,皆圍繞射線旋轉。就像被稱為旋量的數學物件,這種扭曲是透過在射線上附加旗子,從而使其方向清晰而被注意到。
射影幾何學與複數融合的另一個令人欣喜的結果,是時間之矢的更加清晰的畫面。雖然沒有什麼比過去發生的事情和尚未發生的事情之間的區別更明顯,但這種區別無論是從幾何角度還是從物理學角度看並不明顯。舉一個物理學的例子,想象一下早晨的太陽使一片霧氣變暖。當陽光擊中霧中的水分子時,水分子會被加熱,開始以漸增的能量四處運動。隨著分子四處運動並撞擊其他分子時,雲團擴充套件,密度降低,直到雲最終蒸發。但是,把注意力集中在水的分子反彈上,晨霧的大畫面就消失了。如果只拍攝了幾個分子的特寫電影,人們就無法分辨電影放映是向前還是向後,因為物理學定律不會區分跑向未來的事件還是跑向過去的事件。在區域性上,即使霧總體上正在消散,分子的碰撞也能將霧凝聚成孤立的斑點。在這個例子中,有一個清晰的全域性時間之矢和一個混亂的區域性時間之矢。
也存在相反的情形。人們可以透過考察光線的自旋,在區域性檢測光線,看看它們是向前移動,還是向後移動。右旋螺釘被標記為正且隨時間向前移動,左旋螺釘被標記為負且隨時間向後移動。現在,問題在於構建全域性箭頭(global arrow)。彭羅斯解釋道,“量子場論需要把諸場量分解成正頻和負頻部分。前者順時間傳播,而後者逆時間傳播。為了得到理論的傳播子,人們需要一種把正頻率(也就是正能量)部分挑出來的辦法。扭量理論是完成這種分解的一個(不同的)框架——事實上,這種分解正是扭量的一個重要的原始動機” (Hawking and Penrose 1996,107 頁)。
彭羅斯詳細敘述了 1963 年 12 月 1 日一次駕車旅行的確切時刻,當時他意識到,有一種方法可以將這些區域性觀測結果構造成一個完整的全域性圖景,用來描述時間箭頭(arrow of time)。他認識到,實線將複平面分為正虛部和負虛部,這種基本的分解也是用黎曼球面來模擬的。從北極向南半球上的點的投影等同於負頻率,隨時間向後退行,而從北極向北半球上的點的投影則等同於正頻率,沿光錐上部的方向(反天對映)隨時間前行。這一分析給出了時間方向的全域性圖景。彭羅斯宣告:“我找到了我的空間!”(1987 年,第 8 節;2004 年,993 頁以後)
通向實在之路
天球只定義了時空中的一個點,即觀者在當前時刻的位置。光錐的所有光線在時空中的單個點匯聚。因此,每個扭量只定義單個點。問題變成如何將這些點組裝成由離散元素組成的協合空間,以及如何在沒有已有的座標系的情況下做到這一點。換句話說,我們的目標是定義一個空間,首先它具有量子粒度(quantum graininess),因此不是無限可分的;其次它完全由自身組成,而不涉及任何其他系統。按照物理學家的說法,此種空間應該是組合空間,與背景無關。早在 1958年,彭羅斯就提出了自旋網路(一個帶有內部計數系統的拓撲拼砌)的概念來表達這樣的空間。到 1968 年,他開始發表這一觀點,十年後,自旋網路在數理物理學界中廣為人知。彭羅斯將這一想法描述如下:
這裡描述的理論中出現的“方向”皆由系統之間的相互關係所定義,它們一般不會與先前給定的(且是不必要的!)背景空間中的方向一致。在這裡獲得的空間,將被認為(確實必須被認為)是由系統本身決定的空間。希望對上述方案的一些修改能夠考慮到諸系統相對速度的影響,從而也許可能建立四維時空。(上述理論中不含時間,甚至到事件的時間順序與此無關的程度!)(Penrose 1979,306 頁)
自旋網路後來的發展證明,在大型聚集體中,它們的外觀和功能類似於空間,因此與經驗是相容的。該方案的各種修改已經發展,包括高維自旋泡沫。但是,目標仍然是“得到那種完全離散的、明顯是‘組合的’理論框架……要深入到大自然的最微細緻尺度上來理解其運作機制,這一框架是必不可少的”(Penrose 2004,958 頁)。
彭羅斯對扭量的希望是,它們可以用來彌合當代物理學中相對論和量子物理學之間最嚴重的鴻溝,首先把它們放在同一個編號系統中;還有一個很大的鴻溝要跨越;量子物理學是關於過去的故事;後向光錐描述因果過去。如前所述,所有可能影響當前時刻的事件都必須在光錐內,因為只有這樣,任何資訊或影響才有時間到達當前時刻。過去在光錐外發生的任何事件,都必須以比光速更快的速度在當前時刻到達指定的地點。從相對論者的觀點來看,物理學是關於未來的故事。事件受到引力相互作用的影響,此時此刻質量扭曲了局部空間,從而改變了未來。未來光錐向引力質量傾斜;甚至類時間路徑(在空間中沒有任何方向,但只是透過時間)向質量傾斜。
量子力學的佯謬在於,過去光錐之外的事件似乎確實影響(即糾纏)在當前時刻所做的測量。為了解釋因果關係錐外部事件的佯謬,一種流行的觀點認為光錐必須是模糊的(fuzzy);它們朦朧的表面,包括可能被誤認為在光錐之外的點。彭羅斯設想,存在許多毗連的、疊加的光錐,事件是模糊的,直到它們卡入其中的一個或另一個:“在扭量處理中,則是‘光線’未變但‘事件’變得模糊。” (Penrose 2004,966 頁)這種量子多重態(quantum multiplicity)透過“水平大約為一個引力子(gravitron)或更大的尺度”的引力相互作用,被分解成明確的經典結果(Penrose 1989,367 頁)。
另一項建議是認為光錐是剛性的,這樣,傾斜未來光錐也會傾斜過去光錐,從而掃進光錐並導致外部的因果過去事件。如果人停下來想一想,光錐的剛性旋轉是完全反直覺的:過去就是過去,一去不復返,而未來則受當前事件的影響。從現在開始的事件,沒有理由影響過去的情況;毫無疑問,光錐應該會在其夾點處合上。當然,如果光錐由空間中的線組成,它們就會分裂。我建議將光線解釋為射影直線,解釋光錐在旋轉時如何保持剛性。從零射線的角度來看,從過去到現在到未來的路徑不可能有分離,因為這些點之間沒有距離。光線的射影性質意味著光錐不能在其夾點處合上,因此必須是剛性的。使未來光錐傾斜以改變可能的未來不可避免地使過去光錐傾斜,將光錐以外的事件帶入因果過去(圖 10)。
圖10 旋轉一個剛性光錐,會將光錐之外的事件帶入因果過去。
彭羅斯的扭量綱領,可以概括為主要基於三個洞見。他意識到,光線的路徑更像是射影直線,而不是空間中的直線,洛倫茲變換也可以作為莫比烏斯變換來完成,而光錐的完整圖景(緊化圖景)將它們描繪成三維球面上連在一起的平行圓圈(霍普夫纖顫)。接下來至少有四個有希望的結果。所有的物理學,包括相對論,都可以使用相同的複數作為測量系統。粒子中自旋的起源,被看作幾何學的函式。全域性時間之矢,及其對熵(entropy)的影響,與空間的描述結合。最後,這一扭量綱領保證了一個與背景無關的空間組合結構。彭羅斯承認,儘管這個龐大而未完成的扭量綱領目前在純粹數學領域取得了比物理學更全面的成功,但研究人員各自仍在繼續研究這個綱領的不同部分。自旋網路連同其對非連續空間的描述,尤其鼓舞人心。此外,在過去兩年裡,愛德華· 威滕(Edward Witten)找到了一種把扭量和絃理論結合起來的方法,透過這些思想的融合,他可以在更可信的四維,而不是弦理論通常的十一維上搞弦理論。
雖然彭羅斯經常被貼上柏拉圖主義者的標籤,因為他專注於幾何學的首要地位來定義什麼是可能的,但彭羅斯實際上更像一個亞里士多德主義者,他堅持認為我們所觀察到的就是實在,我們的問題來自應用了一些錯誤的模型。“對於那些時空維數超出我們直接可觀察(即1+3)的理論,”彭羅斯說,“我看不出有何理由值得相信,它們使我們背離了物理學認識的方向。”(Penrose 2004,1011 頁)彭羅斯有時又說,扭量只是一種替代表述:“它可能被簡單地看作為解決標準物理理論中的問題提供了新的數學方法。”相反,扭量可能被視作為所有物理學基礎提供了一個替代框架,其特點是“事件概念(時空點)從主要角色降到次要角色”(Penrose and Rindler,第 2 卷, viii 頁)。在這個表述中,扭量的價值是深遠的;彭羅斯想要用反直覺的複數和射影來換取反直覺的高維。既然它們在數學上等價,就採取更接近我們體驗的空間模型。射影模型(projective model)把我們從錯誤的空間概念中解放出來,使我們走上了通向實在之路(The road of reality)。