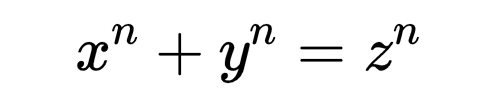對大多數人來說,數學以算術開始,以代數或微積分結束,但數學的範圍比你想象的要大得多。
- 雪花的六重對稱性是水分子對稱性的直接結果,可以透過現代代數來研究。
對許多人來說,數學無非就是算術、幾何、代數和微積分。即使是像工程這樣的技術性較強的學科,也只會在列表中加入微分方程、偏微分方程、統計學,也許還有線性代數。而且,儘管這些數學子領域相當重要,但它們遠遠不是數學的所有。
數學課的主題
在開始之前,我想強調一條特別的線索,它幾乎出現在所有的高等數學課上:證明。在非數學專業的數學和數學密集型課程中,你的大部分精力都花在學習:
- 如何為一個問題建立一個模型。
- 寫出一些適合該模型的數學公式(通常是微分方程或線性方程組)。
- 然後按照一套特定的步驟來獲得相關資訊。
在更高層次的數學課上,你還必須證明一些東西,在這種情況下,你的大部分精力都花在學習:
- 如何為一個問題建立一個模型。
- 寫出一些適合該模型的數學知識(通常是某種函式或演算法)。
- 然後按照一系列特定的步驟來證明這個陳述。
你可能會注意到,這些步驟相當相似,這並不是巧合。雖然證明和計算密切相關,但人們往往更經常地與計算打交道,因此不熟悉證明中使用的技術。出於這個原因,許多大學要求數學學生上一門課,重點是如何寫證明。大學將這門課稱為高階數學入門。非數學專業的學生可能不會上這門課,我不會在本文中提到它,因為它本身不是目的,我想寫一篇關於如何在數學中證明“東西”的文章,類似於我為基礎物理學寫的那篇文章。
邁出成為物理學大師的第一步,應該這樣去求解物理學問題
下面是一個數學學生在微積分、微分方程和偏微分方程之外可能選修的不同科目的清單,這些科目包括什麼,以及每個科目的實際用途。要明確的是,這並不意味著數學需要有直接的實際用途才值得學習。數學本身就很美,而數學發明可能需要幾個世紀的時間才能變得不僅實用,而且必不可少,數論是現代密碼學的基礎,就是一個典型的例子。
離散數學
讓我們從離散數學開始。微積分處理的是平滑、連續的函式,而離散數學則是一個廣泛的領域,涉及任何可以被分離成離散物件的東西。所有計算機科學系學生和電氣工程師都必須上這門課。在標準的課程中,會涉及形式邏輯、計數問題和圖論(不是像f(x)=x^2這樣的圖,而是更像城市和道路的圖,它們都是有向無環圖)等主題。這門課往往是學生們必須證明的第一門課(也是最後一門)。
我們什麼時候會用到離散數學?
正如我已經說過的,離散數學是電氣工程和計算機科學的必修課。在電氣工程中,控制一個電路的每個部分獲得多少電流需要使用圖論,而實現數字邏輯需要使用形式邏輯。計算機科學中的大量問題涉及到識別何時可以用圖來模擬一個系統,然後使用圖論中的一些東西來簡化問題。例如,谷歌的網頁排名演算法將網頁建模為節點,將連結建模為有向邊,然後它可以使用圖論來研究。
計數問題可能看起來沒什麼用,但它們在機率論和統計學中出現得很多。在統計力學中,熵將允許你把尋找一個系統的各種物理屬性(如體積、能量、成分、熱容量等)之間的關係的問題轉換成一個計數問題,正如你可以在文章從零推匯出理想氣體定律,一項浩大的工程,涉及數理化三個領域中看到的那樣。使用統計力學將熱力學問題變成計數問題的最典型的例子必須是愛因斯坦模型。
愛因斯坦模型是晶體固體的模型,它包含了大量的相同頻率的獨立三維量子諧振子。在德拜模型中,獨立性假設是鬆弛的。
實分析
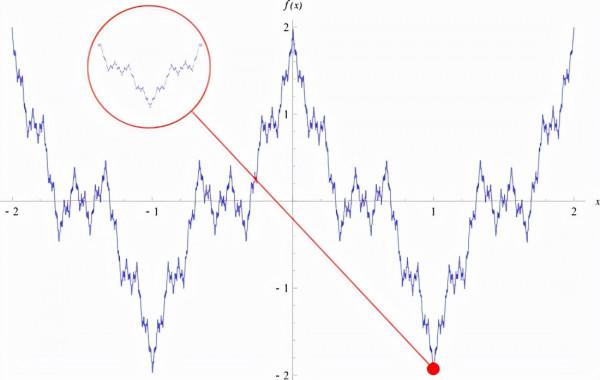
我們已經介紹了離散數學,讓我們來看看微積分的核心——實分析。在微積分發明後的幾個世紀裡,人們開始注意到,很多我們認為理所當然的關於微積分和實數的事情並不真實。例如,一個函式在任何地方都是連續的並不意味著它在任何地方都是光滑的。這些假設導致了一些證明,這些證明聲稱可以證明所有具有某種屬性的函式(如所有連續函式)的定理,但只適用於部分函式(如所有利普希茨連續函式)。為了解決這些混亂的問題,人們想出了實分析。這是一個重要的領域,它為所有的微積分提供了論證。
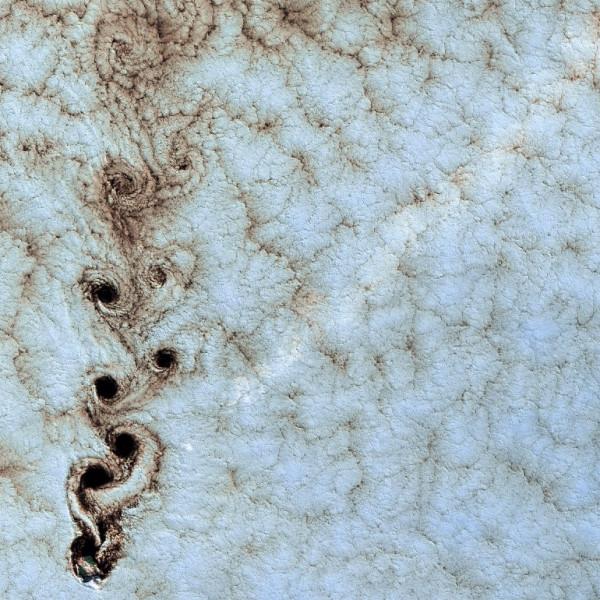
- 弄清圖片中湍流背後的數學原理,就能得一百萬美元。
我們什麼時候會用到實分析?
實分析在告訴你一個函式到底有多好,這對於確定你可以用什麼技術來解決一個問題,以及這個問題是否可以解決是很有用的。作為一個典型的例子,納維爾-斯托克斯方程構成了流體力學的基礎,類似於麥克斯韋方程構成了電磁學的基礎。
改變世界的方程之納維爾-斯托克斯方程,堪稱最難的物理學方程
麥克斯韋方程,19世紀最偉大的發現之一,現代物理學的基礎支柱
與麥克斯韋方程不同,我們尚未證明納維-斯托克斯方程在任何初始條件下都存在光滑解。證明或否定納維-斯托克斯方程總是有光滑的解,是物理學中最大的未決問題之一。實分析和函式分析(建立在實分析的基礎上)對於理解和解決這個問題是必要的。
對於那些不是數學物理學家的人來說,你可能不會從實分析中得到那麼多。現實世界中的常見函式往往是“良好”的,所以你通常可以假設有人已經在背後做了實分析的工作。
複分析
- 黎曼zeta函式圖
當人們(例如柯西)在研究實分析時,也在研究複分析,複分析將實函式擴充套件到複平面。實分析和複分析之間的一個重要區別是,複分析對它所處理的函式種類更加“挑剔”。
雖然這種挑剔性限制了複分析可以處理的函式,,但它可以對它可以處理的函式做更多的事情。例如,它允許你做一些在實線上很難做的積分。
我們什麼時候會用到複分析?
複分析出現在許多你意想不到的地方。想知道素數的分佈嗎?你需要找出黎曼Zeta函式的零點。想找到一種方法來穩定一個不穩定的系統?你需要找到一些方法,將系統的傳遞函式的極點向左移動。像拉普拉斯變換、傅立葉變換、傳遞函式和z-變換這樣的概念要依靠複分析來理解。
現代/抽象代數
這個領域研究符號和對符號的運算。在這個領域出現的一般問題是,如果你有一個物體,你對這個物體進行了一系列的操作,你能找到一些方法來 "撤銷 "這些操作嗎?你能解出一個給定的x方程式嗎?你可能習慣於x是一個實數或複數,你有一些多項式方程,如x^2 - 2x + 5 = 0,但如果x和所有的乘法,加法,減法的結果都只能是0到10之間的數字呢?在這種情況下,你要處理的是11階的有限域。特別值得注意的是階為2的有限域,它是計算機的基礎,因為你可以把加法變成排他性或門,把乘法變成和門。
我們什麼時候會用到抽象代數?
現代代數有許多子領域(如群論、線性代數),並與其他領域(如代數拓撲學和代數數論)有交集,這使得有點難以單獨談論它。由於線性代數是一門獨立的課程,我將在其章節中談論它。
假設有人交給你一個分子,你想預測它的特性。你可以看幾個特徵,比如鍵的型別、組成原子的質量、自由電子的分佈等等。這些特徵之一是由分子顯示的所有對稱性組成。要研究它們需要抽象代數。
魔方不需要介紹。在電影《當幸福來敲門》中,解開魔方的能力是一種挑戰,只有智力高超的人才能做到。在現實生活中,任何人都可以透過記住一些演算法來複原魔方。但是,你會如何找到這些演算法?第一步應該是想出一個數學模型。在這種情況下,如果你把每個旋轉看作是一個運算,那麼解魔方就相當於 "撤銷 "旋轉,這意味著你可以在這個問題上使用抽象代數的工具。
線性代數
我的電腦目前有以下配置:
- CPU:AMD Ryzen 7 2700X
- GPU:NVIDIA GeForce GTX 1660
- 記憶體:2 x Corsair Vengeance 16GB DDR4
- 固態硬碟:三星860 EVO 1TB
- 鍵盤:海盜船遊戲K55 RGB鍵盤
- 滑鼠:羅技G502滑鼠
計算機的每個部分大多獨立於計算機的其他部分。如果我想要更多的記憶體,我不需要買一臺新的電腦,我只需要增加一個固態硬碟。同樣,我可以用任何其他滑鼠替換我的滑鼠,或者用任何其他具有相同介面的CPU替換我的CPU。當一個系統由可以改變而不改變任何其他部分的部件組成時,我們稱之為模組化系統。
計算機遠不是唯一的模組化系統。自工業革命以來製造的大多數產品都是模組化的,因為處理大量簡單的模組化事物比處理少量複雜的相互連線的事物要容易得多。這一認識導致了線性代數領域的出現。類似於複分析將其重點限制在某些種類的函式上,線性代數將其重點限制在代數結構上,,在這種結構中,將一個操作應用到一個物件上,就像將操作應用到它的各個部分上,並將結果相加。
如果你能證明一個系統或運算是線性的,問題就會變得容易得多,因為你可以把物件分解成它的各個部分,進行運算,然後把所有東西再加起來。
我們什麼時候才會用到線性代數?
導數和積分是線性運算子,因此你可以使用線性代數的工具來分析它們。與其把7x^2 + 5x^4的導數塞進差分商中(求導),你分別對x^2和x^4求導,再分別乘以7和5,然後把它們加在一起,得到14 x + 20 x³。不過,直到你遇到微分方程,線性代數的優勢才變得明顯。一旦你遇到偏微分方程,你將開始解決特徵值方程,這與你線上性代數中看到的特徵值方程幾乎相同。在量子力學中,這些特徵值具有特殊的意義:它們代表了你可以觀察到的給定系統的可能值(表述做了很多簡化)。在微分幾何中,你最終要處理的是多線性對映(又稱張量),它是你線上性代數中看到的線性對映的概括。最後,函式分析是實分析的延伸,可以認為是線性代數在函式空間的應用。
線性代數在統計學和機率學中也有大量的應用,最典型的例子是線性迴歸和期望值的線性化。線性代數也出現在分析馬爾科夫模型中,這些系統根據其當前狀態和一組機率在多個狀態之間轉換。例如,你可以使用馬爾可夫模型來估計一個人在大富翁遊戲中落在一個特定方格上的機率。
如果你對人工智慧研究感興趣,你會發現其中有大量的線性代數。尋找線性迴歸是現代人工智慧演算法的先驅,早在計算機出現之前就已經發明瞭。現代演算法,如主成分分析,透過用線性代數找到的新變數來重寫資料,並丟棄那些不能解釋大量方差的變數。除此之外,隱馬爾可夫模型依賴於馬爾可夫模型,正如我之前所說,它依賴於線性代數。
我第一次學習化學時發現的一個應用是,可以透過把化學方程式寫成線性方程組來配平。對我來說,這個過程減少了我必須記住的一系列步驟,只是 "寫出方程組,並將其插入計算器"。如果我把線性代數的所有可能用途都寫出來,這篇文章要花好幾天才能讀完,所以就到此為止。
微分幾何學
微分幾何學是研究光滑事物的幾何學,包括曲線、曲面和流形。例如,是否有可能在不拉伸或壓縮球體的任何部分的情況下將其壓扁?如果是這樣,那麼我們就可以製作一張沒有失真的地球平面圖。高斯使用微分幾何證明了任何地球地圖都必然有扭曲。
我們什麼時候會用到微分幾何?
製圖學很酷,這一領域在物理學上有特殊用途。愛因斯坦的一個假設指出,所有的慣性參考系都應該遵守相同的物理定律,這意味著我們需要一些一致的方式來描述座標系的變化。微分幾何學可以告訴你座標系的變化對數學有什麼影響。出於這個原因,物理定律必須用張量來表述,張量使用微分幾何的規則來抽象出座標系,同時保持相同的物理學。如果你聽說過彎曲的時空,你就會用微分幾何來研究這種曲率。如果你想做任何高層次的物理學,你應該對操作張量得心應手。
機率與統計
你一定聽說過機率和統計。你們中的大多數人都能回答一些基本的機率問題。統計學可能比微積分更適用於一個人的日常生活。
我們什麼時候會用到機率與統計?
從根本上說,科學不過是根據你所知道的東西進行預測,而在任何科學領域進行定量預測都需要數學。在許多科學領域,微積分和密切相關的微分方程領域構成了該領域的基礎方程式。沒有麥克斯韋方程,你根本不可能掌握電磁學。另一方面,科學需要實驗,而對實驗結果的正確解釋需要統計分析。你怎麼能知道你是否發現了希格斯玻色子,或者只是得到了一些看起來像希格斯玻色子的資料?
當然,機率和統計學並不僅僅用於解釋和分析資料。在某些領域,機率和統計是基礎。統計力學需要使用機率和統計學(以及微積分),但統計力學本身是許多科學領域的基礎,包括熱力學、固態力學、化學等。因此,這些依賴統計力學的領域必須依賴機率和統計學。量子力學指出,宇宙在基本層面上是機率性的,因此需要機率和統計學來理解。
它對於量化確定性、計算出一個合適的樣本量、在撲克比賽中贏得很多錢、理解為什麼你在賭場中可能會輸錢等也很有用。
人工智慧和機器學習只是高階機率和統計學。任何基於馬爾科夫過程的東西從根本上說都是基於機率和統計的,這包括人工智慧演算法,如隱馬爾科夫模型。甚至神經網路本質上也是非線性迴歸。
數值方法
方程對於觀察一般趨勢來說是很好的,但在幾乎每個領域,你都需要插入數值來得到一個數字結果。在數值方法中,你將學習如何在儘可能短的時間內獲得準確的結果。數值方法還可以根據你使用的任何資料來量化你所使用的任何數值方法的不穩定性,這可以幫助你選擇合適的工具來完成工作。
我們什麼時候會用到數值方法?
有很多問題,解析解要麼不存在(解決次數大於4次的多項式),要麼不方便計算(某些型別的微分方程),這就需要數值方法了。
- 牛頓法是解方程的標準演算法。它還能做出一些看起來很酷的分形圖。
- 尤拉方法是模擬由帶初始條件的微分方程支配的系統的起點。
- 有限元分析將模擬一個由帶有邊界條件的微分方程控制的系統。它本身就是一個完整的領域。
- 有大量的積分方法(辛普森規則、高斯求積法等)具有不同的特性,可以快速計算任意積分。要知道對一個特定的函式可以使用哪些積分方法,需要進行實分析。
- 高斯消去法是解決線性方程組的大多數實用演算法的基礎。為特殊型別的系統尋找演算法需要線性代數。
只要你需要能夠快速計算,你就需要使用數值方法。例如,影片遊戲特別需要實時近似物理,所以它們經常使用具有中等精度的快速方法,如半隱式尤拉法。
其他課程
有幾門數學課程我在本科時沒有學過,我只能提供一個簡單的概述。
拓撲學
拓撲學是關於當你對一個物體進行變形而不將其撕裂(穿孔)或將其部分粘在一起時,什麼東西保持不變的問題。一個著名的例子是,在拓撲學中,你不能把咖啡杯變成一個球體,但你可以把它變成一個甜甜圈。
我們什麼時候會用到拓撲學?
雖然我在本科沒有學過拓撲學,但我在離散數學、實分析和微分幾何中接觸過它。我的離散數學課程專注於圖論,這是拓撲學中最早的課題之一。能否在沒有交叉邊的曲面上繪製圖形取決於曲面的拓撲結構。連續性和度量空間是實分析和拓撲學的重要課題。最後,尤拉示性數(一個與曲面的拓撲結構有關的數字)對微分幾何中某些積分的值設定了限制(見高斯-波內特定理)。
數論
數學是科學的女王--而數論是數學的女王——卡爾-弗里德里希-高斯
數論是現代代數的一個子集,專注於與整數有關的問題,特別是素數分佈的問題,如哥德巴赫猜想和孿生素數猜想。數論是一個不尋常的領域,因為你可以向一個普通人解釋大部分問題,但很少有證明的問題。例如,費馬大定理說這個方程沒有整數解:
當n>2時。費馬大定理的證明是一個漫長而曲折的旅程,需要幾個世紀的數學知識。數論是一個特別困難的領域。數學家們經常想出強大的新技術和想法來解決數論中的問題,而這些技術和想法經常被應用於其他領域。
我們什麼時候會用到數論?
數論是現代密碼學的基礎,以及許多證明依賴於黎曼假設的結果。
這裡有幾個專業學習建議
非電氣工程師
我推薦這些課程:
- 線性代數
- 數值方法
- 複分析。它在控制理論等方面很有用,可以分析系統對輸入的響應,並做某些型別的積分,但大多數相關的東西都是從該領域提取的,並提煉成工程師的課程。對於非電氣工程師來說,複分析是邊緣的,因為它可以給你一些技術,使你的工作更容易,但它不是必要的。
電氣工程師
對於電氣工程師來說,我推薦以下課程:
- 離散數學。邏輯閘和布林代數是形式邏輯的一種應用,所以你必須要選離散數學。在此基礎上,電路設計是應用圖論。
- 線性代數。電路中的電流和電壓常常需要一個線性方程組。另外,疊加法也需要線性代數。
- 複分析。鑑於電感器和電容器有複數阻抗,而且EE經常要處理交流電,複數分析是相當有用的。
- 現代/抽象代數。
計算機科學家/程式設計師
對於這個領域(包括人工智慧、生物資訊學等),我建議選擇:
- 離散數學。這是學位的要求,圖論知識對這個領域至關重要。
- 數值方法/線性代數。
- 如果你從事的是密碼學工作,請將數論加入到學習計劃中。
物理學家
我推薦:
- 線性代數。你將花大部分時間與線性系統打交道。
- 微分幾何。物理學定律是用張量來寫的。
- 複分析。不必多說。
不同的領域有不同的專業。例如,很多高階物理學變成了現代代數(SU(3)指的是3階的特殊單元組),計算物理學需要數值方法的專業知識,而實分析是數學物理學的基本內容。
其他所有人
如果你的專業還沒有被提及,那麼你可能應該選修機率和統計學。如果你已經被提及,那麼你應該選修機率和統計學。透過形式邏輯,我們可以得出結論,你應該學習機率和統計學。