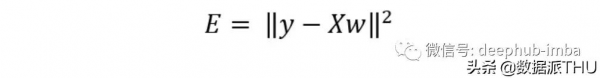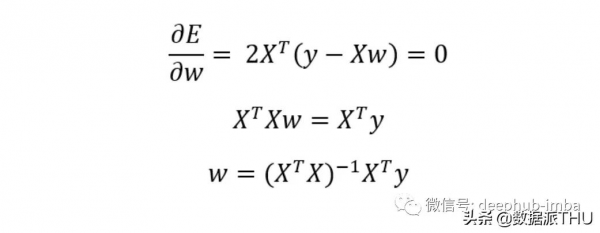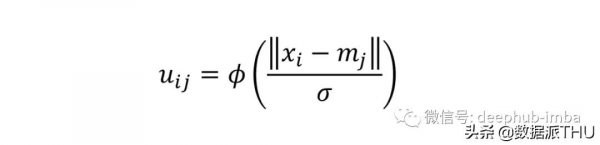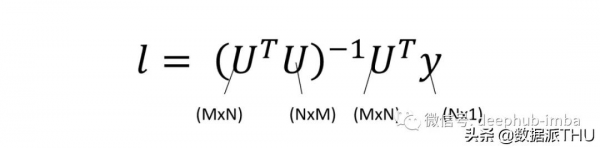來源：Deephub Imba
本文約2000字，建議閱讀8分鐘 核方法就是透過將資料的輸入空間對映到高維特徵空間，在高維特徵空間中可以訓練簡單的線性模型，從而得到高效、低偏差、低方差的模型。

偏差-方差困境是機器學習方法面臨的主要問題。如果模型過於簡單則模型將難以找到輸入和輸出之間的適當關係（欠擬合）。如果一個模型太複雜，它在訓練中會表現得更好，但在看不見的資料上的效能會有更大的差異（或過擬合），而且複雜的模型往往需要更昂貴的計算資源。對於機器學習來說理想的方法是，能夠找到一個簡單的模型，它訓練起來既很快又可以找到輸入和輸出之間的複雜關係。核方法就是透過將資料的輸入空間對映到高維特徵空間，在高維特徵空間中可以訓練簡單的線性模型，從而得到高效、低偏差、低方差的模型。

這句話就是本文的寫作目的。在看完本文後，希望你能很好地理解這句話的含義以及它為什麼重要。

核方法

機器學習世界中有許多的核方法。支援向量機(svm)就是其中之一，在20世紀後期甚至優於當時的神經網路。但是現在因為資料的數量有了突飛猛進的發展，所以核方法並不佔優勢。因為核方法最適合於中小型資料集，但是在結果的可解釋性很重要的問題上核方法還是有優勢的。

核方法使用核（或基函式）將輸入資料對映到不同的空間。透過這種對映，簡單的模型可以在新的特徵空間而不是輸入空間上訓練，從而提高模型的效能。

以上是對核函式的介紹，在本篇文章中將重點介紹徑向基函式，這是一個非常簡單但常見的核。

線性迴歸和 RBF（徑向基函式）

在迴歸問題中，我們試圖估計從 X 推斷 Y 的最佳函式。如果 X 和 Y 之間存在非線性關係，則不能簡單地在此資料上擬合線性模型。然而，核方法的目標是在這些非線性關係上使用線性模型並保證結果是正確的。

核心方法透過將資料轉換為更高維度並在此維度上擬合線性模型來實現這一點。透過這種方法我們在原始輸入空間中有效地擬合了一個高階模型。

線性迴歸

我們先看一下線性迴歸，然後我們就可以瞭解如何使用核方法對線性模型生成非線性對映。

最優線性迴歸是最小化我們模型的預測和目標輸出y之間的平方距離的迴歸器。將這個誤差最小化就能得到最優解決方案。

我們可以將最小二乘誤差與我們模型的權重進行微分，從而找到產生最小誤差的權重向量，結果就是偽逆解。為了正確理解線性代數公式，我們必須熟悉每個變數的維度數：

輸入資料 X 是 (Nxd) 維，其中 N 是資料點的數量，d 是特徵的數量。因此，逆計算將是一個 (dxd) 矩陣，並且所得的權重矩陣是 (dx1)。我們的權重向量與輸入資料中的特徵具有相同的維度。這是肯定的，因為當我們從 X 推斷 Y 時，我們採用權重和輸入資料之間的點積，因此輸入必須具有與我們的權重相同的維度。

高維空間中的線性迴歸

核方法透過使用核或一組 M 個基函式將資料矩陣 X 對映到新的設計矩陣 U（design matrix）。新的設計矩陣具有更高的維度（NxM，其中 M ≥ d）。

我們可以透過採用 M 個基函式 (ϕ) 來構造一個設計矩陣 U，每個基函式都由它們自己的均值和標準差引數化。上面等式中的平均值的維數為 (dx1)。因此，對於輸入空間中的每個資料點，我們應用 M 個基函式將輸入維度 (Nxd) 轉換為新的設計矩陣 (NxM)。

RBF 使用高斯基函式。每個基函式代表輸入空間中的高斯分佈。每個資料點都在所有高斯分佈中進行評估。結果是輸入向量從 d 維到 M 維的對映。

要引數化這些高斯分佈的均值和標準差，可以使用k-means聚類得到引數化基函式的均值和標準差。

現在我們有了我們的設計矩陣 U，並且我們已經將輸入資料對映到了一個高維空間，我們可以在這個新的特徵空間中擬合一個線性模型。

透過來自特徵空間的估計和我們的目標 y 之間的最小二乘誤差，並根據我們的新權重向量 l 進行微分，我們發現最優解與輸入資料中線性迴歸的最優解相同。

這裡要注意的是我們的權重向量 (l) 現在是一個 Mx1 向量，在原始輸入空間中，權重向量是一個 dx1 向量（記住 M > d）。

合成數據的例子

這是合成的非線性資料。有 10,000 個數據點，我們的 Y 座標是一維的。這意味著我的資料矩陣 X 的維度為 (10,000x1)。我們可以嘗試透過使用上面看到的偽逆解計算最佳權重來擬合該資料的線性模型。正如您在上面看到的那樣，它的表現並不好。

下面我們透過在高維特徵空間中擬合相同的線性模型，更好地近似資料中的真實關係。

首先，我將 200 個基函式應用於我的每個資料點。我在我的輸入空間中採用 200 個高斯分佈，並評估我所有基本函式的每個資料點。我的新設計矩陣現在是 (10,000x200) 維的。然後我使用相同的偽逆解來獲得這個新特徵空間中的最佳權重。

RBF模型估計的關係是非線性的，並且與資料吻合得很好。但是這個新模型仍然是一個線性迴歸器！因為我們將它擬合到新特徵空間中，所以我們間接地在原始輸入空間中擬合了一個複雜的非線性模型。

總結

核方法使用核（或一組基函式）將低維輸入空間對映到高維特徵空間。並在新的特徵空間中訓練一個線性模型(ax +b型別的線性模型)。我們實際上是在原始輸入空間中訓練一個高階模型(例如ax²+bx +c型別)。透過這樣做，既保留了簡單模型的所有優勢(如訓練速度、具有解析解、方差更低)，也獲得了更復雜模型的優勢(更好的對映、更低的偏差)。這就是核心方法如此強大的原因!

作者：Diego Unzueta