光譜儀器是光電儀器的重要組成部分。它是用光學原理,對物質的結構和成份等進行測量、分析和處理的基本裝置,具有分析精度高、測量範圍大,速度快等優點。它廣泛應用於冶金、地質、石油、化工、醫藥衛生、環境保護等部門;也是軍事偵察、宇宙探索、資源和水文探測等必不可少的遙感裝置。
一. 光譜稜鏡的分光原理
1. 稜鏡色散公式
1665年牛頓發現了光的色散現象,他令一束平行的白光透過一塊玻璃稜鏡,在稜鏡後的螢幕上得到一條彩色光帶。這就是最原始的色散模型。
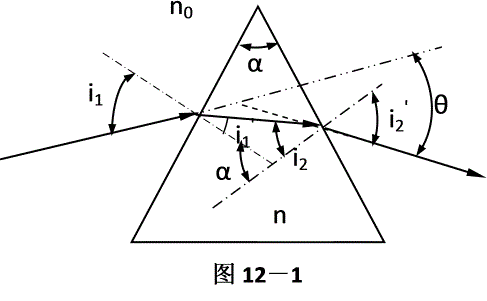
如圖12-1所示是通光稜鏡主截面的光路圖。
它是一個頂角為α的等腰三角形稜鏡。光束的入射方向和出射方向的夾角θ為偏向角。
折射定律為
n0Sini1=n Sini1'
n0Sini2'= n Sini2 ----------(1)
如果稜鏡置於空氣中,n0≈1,則(1)式為
Sini1=n Sini1'
Sini2'= n Sini2 ----------(2)
如圖可見 α= i1'+ i2 ----------(3)
θ=(i1- i1')+(i2'- i2)
= i1+ i2'-( i1'+ i2)
= i1+ i2'-α ----------(4)
將折射角與入射角的關係式(2)代入上式得
----------(5)
由(5)式可見,對於α角已定的光譜稜鏡,當入射角i1不變時,偏向角θ是折射率n的函式。又因為n是波長λ的函式,所以θ隨波長的不同而不同。一束白光經稜鏡後,各波長對應的偏向角θ不同,即在空間上被分解開來,如圖12-2所示。
一般λ↓、n↑、θ↑
( 注:Hartman哈特曼經驗公式
n0 、c和α1都是一些常數,玻璃不同,它們的數值不同。)
2. 最小偏向角條件
函式有一個最小值
將⑷式對
微分
最小偏向角的必要條件是
,則
將⑵式微分:
將上式相除得:
將⑶式微分得
並代入上式得
將此式代入⑹式得:
將上式平方並利用⑵式得:
由⑼式可見,只有當
時,⑼式才成立。
在
時,有:
>0
所以上述條件,也是實現最小偏向角的充分條件。
在最小偏向角情況下,光路對稱,內部光線平行於底邊傳播。
此時
則i1隨n而變,即隨
而變。
二、光譜稜鏡的基本特性
1. 角色散率
不同波長的單色光經過稜鏡後有不同的偏向角θ,
稱為稜鏡角色散率。
將⑷式中
和α作為常量(不變),然後對波長微分,得:
下面求
: 由於
將(13)式代入(12)式
上式兩邊對n微分:
則
角色散率
是稜鏡材料的色散率,它表示介質的折射率隨波長的變化程度。
當稜鏡位於最小偏向角時:
,
由(16)式可見:
有利於
一般α=60°~70°
2. 光譜稜鏡的解析度
兩條譜線波長的平均數與這兩條剛好能分辨開的譜線之間的波長差之比,成為光譜稜鏡的解析度,即
D
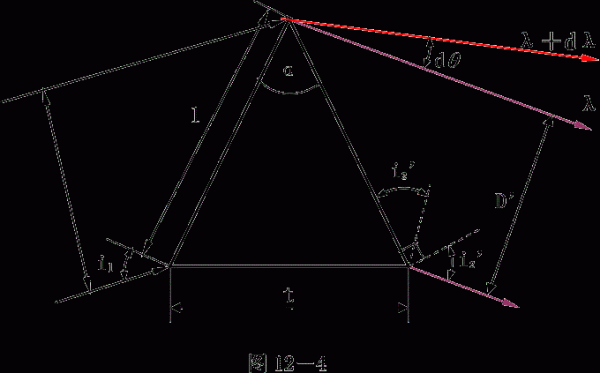
設含有兩個波長(其波長差為dλ)的一束平行光,以滿足最小偏向角條件(i2’=i1)透過圖12-4所示稜鏡,由(16)式,經色散後,其角距離為:
由稜鏡矩孔衍射所決定的最小分辨角為:
而
,則
要能分開兩個波長的光束,根據瑞利判據
兩邊除以dλ得:
解析度:
要增大稜鏡的解析度,可以增大稜鏡底邊長度t,選用介質色散率
大的材料。
三、單色儀系統圖
1.只要保持三稜鏡與平面鏡的相對位置不變(
不變),則處於最小偏向角的光線的總偏向角(
)也不變。
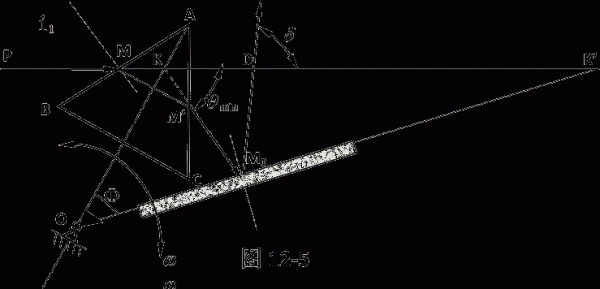
試證:圖12-5所示總偏向角δ與夾角Φ的關係式為:δ=1800-2Φ
證明:∵ 2∠OKM0=1800-
min
∴ ∠OKM0=900-
min/2 (1)
根據反射定律 ∠O M0K= ∠D M0K’
∴ ∠KM0 D =1800-2∠O M0K (2)
而在⊿O M0K中, ∠O M0K=1800-Φ
-∠O K M0 (3)
(1) 代入(3)得
∠O M0K=1800-Φ
-900+Φ
min/2=900-Φ
+Φ
min/2 (4)
(4)代入(2)得
∠K M0D=1800-2[900-Φ+Φ
min/2]=2Φ-Φ min (5)
在⊿KM0D中δ=1800-δ
min-∠K M0D=1800-2Φ (6)
由公式(6)可以看出,只要保持Φ不變則總偏向角δ也不變。即:當入射光線的光軸的空間位置不變(對機架而言),出射光的光軸的空間位置也不變。
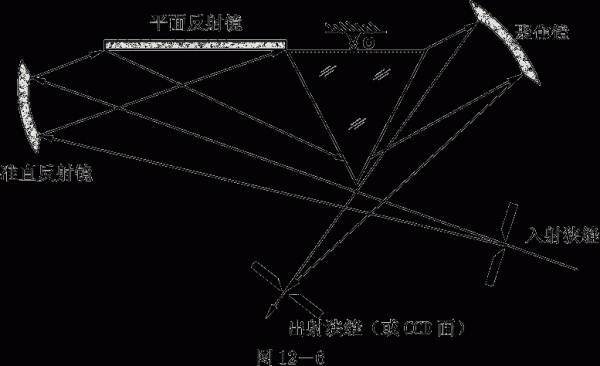
此種稜鏡稱為“瓦茨沃爾脫稜鏡系統”,是一種恆偏向稜鏡(δ不隨波長而變),如圖12-6所示,其中Φ=900,δ=1800-2Φ=00
稜鏡與平面反射鏡一起繞o點轉動,就可以使不同波長的光線以最小偏向角位置透過系統射出。o為折射稜鏡頂角的平分線與平面鏡延長線的交點。
2. 把與平面反射鏡固成一體(Φ不變)繞O點轉動ω,出射光位置不變(見第1條),而此時入射角i1發生了變化,實現了對波長λ掃描。
說明:在最小偏向角條件下 i1’=α/2 (α為稜鏡頂角)
由折射定律 n0sin i1=nsin i1’ (n0=1)
∴ i1=arcsin(nsin
)
i1(n)是n的函式也是λ的函式,對i1掃描就是對λ掃描。
習題1:重火石玻璃稜鏡,α=600,哈特曼經驗公式為
測得λ0=203.457nm,C=14.62336,n0=1.61738,求:λ=404.68nm時的
及角色散率。
習題2:稜鏡的折射率n=1.69, 問:稜鏡的頂角α有何限制?
習題3:圖12-6中,由準直反射鏡入射到平面鏡的光線與平面鏡的法線成600角,採用重火石玻璃稜鏡,頂角α=600,哈特曼經驗公式如習題1所示。求:出射光波長。




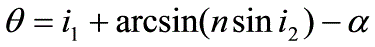
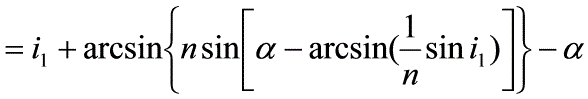






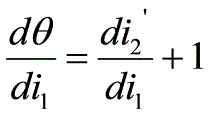
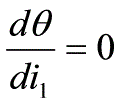


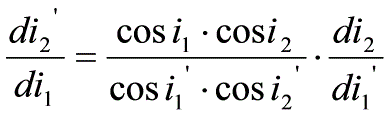



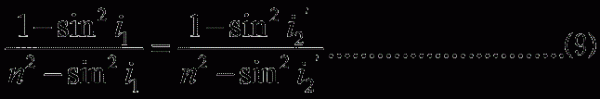

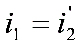



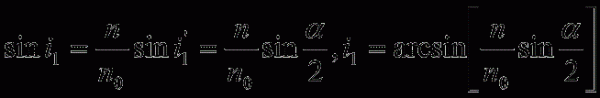





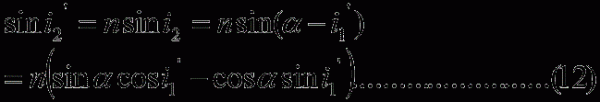
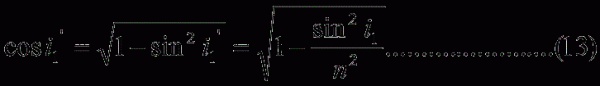


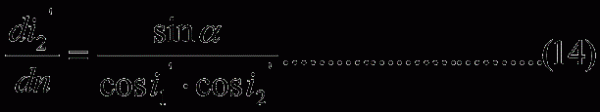
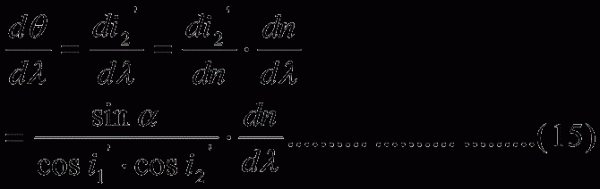
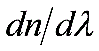
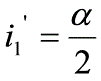


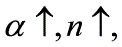
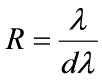

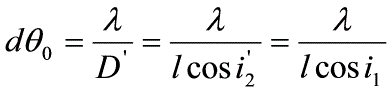

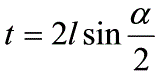
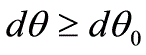

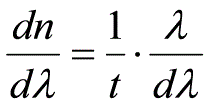
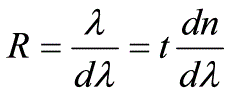







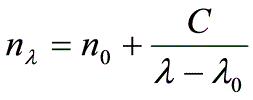


















![[星空有約]今起連續三年中秋“十五的月亮十五圓”:如何賞?怎樣拍? [星空有約]今起連續三年中秋“十五的月亮十五圓”:如何賞?怎樣拍?](http://i.kkannews.com/thumb/280x220/6/ba/6ba05bfc6fee77f08af2df374c86d9ed.jpg)
