伽利略的斜面實驗的疑問

前面一篇文章中有一個實驗，這裡想要仔細的解說一下。

如標題所說，是伽利略的斜面實驗，這裡稍微多說一句，伽利略通常被認為是近代科學的開端。他的探究問題的方法至今還是有很多的應用場景。這裡就是透過對實驗的解說來複盤重現一下思考的過程。

先上實驗

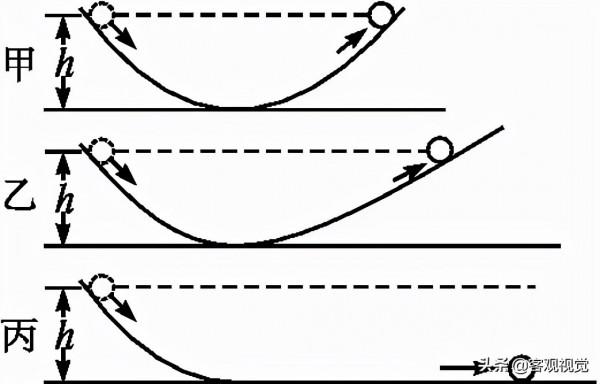
在軌道的一邊釋放一顆鋼珠，如果忽略摩擦力帶來的影響，我們發現鋼珠從左邊滾下後，再從右邊的斜面滾上，鋼珠將上升到與左邊釋放高度相同的點；若將右邊的傾斜角減小，鋼珠還是上升到原來的高度，但透過的路程比原來更長；假設右邊的軌道為水平，鋼珠想要達到原來的高度，但是鋼珠無法達到原來的高度，鋼珠將永遠運動下去。

首先，我們可以參考一些我們生活中常見的場景，比如說，盪鞦韆亦或是鐘擺。還有比如喜歡運動的滑板場地，都有類似的情景，鞦韆在來回蕩的過程通常會越來越低，得有一個人站在後面每次推一下，這樣才能蕩的時間比較長。

鐘擺也需要經歷一段時間後重新調整鐘擺的高度，不然就停下來了。

藉以參考現實中的情況，對於開頭圖中，甲的情況是當小球從左邊滾下來是不可能滾動到右邊相同的高度的。

那麼問題來了，這裡我們是如何處理這種問題呢？

這裡可把問題分解一下，首先是實驗的問題，這個是毋庸置疑的。不可能到相同的高度。再者就是，可以稍微探究一下，是什麼原因導致每次都低一點呢？

這裡其實可以再設計一個實驗，就我們的生活經驗來看，鞦韆在蕩的過程，每次下降的高度是不太一樣的，比如，在比較高的時候，高度下降的比較快，在比較低的時候反而降的慢，可以來回蕩很多回。那回到這個實驗，我們可以嘗試準備，比較粗糙的軌道和比較光滑的軌道，實在不行，在抹點油【在這裡我們的手段儘可能的從經驗出發】哪怕就是經驗也會告訴我們，比較光滑的軌道小球到達右邊的高度會較高一些。如果想要探究的更深一點，可以嘗試不同的材料，總會得出更高的高度。應該也不會高出原來的高度。

到了這裡，其實可以得出一個結論，那就是不管如何改善實驗的條件，小球是無論如何也到不了原來的高度，可改變的就只有不斷的提高右邊能夠到達的高度。這貌似就很無奈了，一般來說我們對自然的印象是固定的，而這個實驗的結果是右邊的小球會上升到接近原來的高度，至於說有多接近，或許會接近到難以測量。

理性來說，能得到這個結果已經很不錯了，但是這個是一個不能稱之為結果的結果。因為依然得到了一個不確定的答案。

上面就是實驗和實驗能夠得到的比較好的結果了。接下來就可以思考和處理上面的事情了，首先這個結果不是太能夠接受的。那麼接下來就透過邏輯思考的方式來對問題進行一個思考。

第一個思路，那就是這個過程是在不斷減少阻力的情況下得到的結果，那麼是不是可以假設如果把這個阻力減少直到到沒有的情況下，小球到達右邊的時候還會上升一點的高度，到達原來的高度。這種思路貌似是可行的，但是還不夠嚴謹。(這是極限思想)

第二個思路就是，宏觀來看，小球的情況是接近原來的高度，是不是就可以假設小球有上升到原來高度的潛質，導致小球有不斷衝擊到原來的高度，而這種潛質因為阻力消耗了部分。（後面的能量守恆）

聽懂掌聲

到了這裡，不妨大膽想象一下，就預設小球在無阻力的情況可以到達相同的高度。實際上，在這裡的處理方法是在考察實驗的情況對實驗的結果做適當的延伸，來得到一個理想的結果。至於這個結果是不是正確的在這裡的純邏輯的角度下是很證明的。但是，可以在後續的討論中，以這個為基礎，如果從它推出的結果是正確的，那麼可以間接的證明這個的假設是合理的。

以上就得出了一個結論，那就是小球從左側滾來了，在非常理想的情況下(無阻力，無干擾）滾動到右側的時候可以達到相同的高度。

那麼在理想情況下，如果將右邊的斜邊緩慢的降低角度直到平鋪，由於小球無法達到原來的高度，因此也會一直向右邊運動下去。

觀察小球在右邊的運動，也就是得出一個結論，在無干擾的情況下，小球將一直做直線運動，

ⅰ：理想情況速度是不會增加的，（如果增加，那麼在上述實驗過程小球在到達右邊的時候會高過原來的高度）

ⅱ：理想情況速度是不會減少的，（如果減少，那麼在實驗中小球會停下來，在推理過程中小球不會停下）

因此也可以推匯出牛頓第一定律，在沒有外界干擾的情況物體會做勻速直線運動或者靜止。

證明完畢。

牛頓第一定律是相對難以理解的，一度也被稱為理想定律，其實是因為在現實中，很難透過實驗來對定律進行驗證，在我們身邊找不到不受干擾的情況，在對第一定律的直接驗證試驗是在宇宙飛船空間站中進行的驗證。

第一定律在平時的使用其實也不多，更多的好像可以來解釋一些事情，其實，第一定律的作用是奠定了經典物理的基礎，因為，他還有一個名字叫慣性定律，給出了在沒有干擾的情況下物體的狀態，使得後面的物理問題研究和對物理量的測量有了一個明確的標杆，從此有了參考系的概念。

今天就到這裡，如果各位感興趣或者有期待就請點選關注