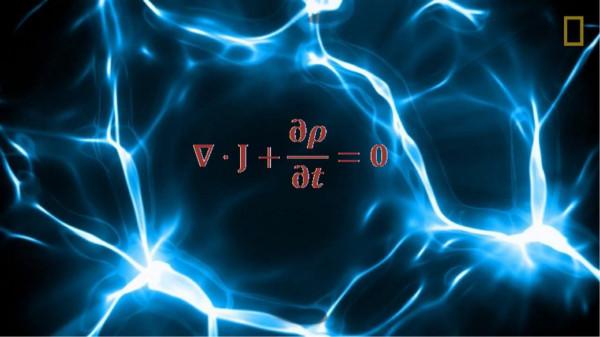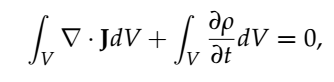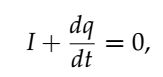電磁學中極為重要的連續性方程，一個簡單的證明

連續性方程在物理學中是至關重要的，因為它告訴我們什麼物理量在什麼條件下必須守恆。就電磁學而言，必須守恆的最基本的量是電荷q，即流經空間某一區域(如電流)的總電荷量。連續性方程為：

• 方程1：微分形式的電荷的連續性方程

其中

是電流密度J的散度（是流過某個橫截面積的電流量）和

是電荷密度在空間各點相對於時間的變化率。這是通量守恆的直接結果。我們也可以在積分的背景下看這個表示式：在方程的兩邊對體積進行積分，可以得到：

利用導數和積分是線性運算子的事實，我們可以從第二項的積分中取出時間導數。此外，透過對第一項應用散度定理，我們可以將方程改寫為：

• 方程2：積分形式的電荷的連續性方程

仔細觀察這個表示式，我們發現第二項的積分只是封閉表面S內的總電荷，即q，而第一項的積分只是電流I，結果是：

• 方程3：電荷守恆

這就完成了證明。方程1中的連續性方程在電磁學中極為重要，特別是電磁波傳播和輻射。