這節課講解:在二次函式y=ax²+bx+c中,如何根據圖象判斷2a+b、2a-b、4a+b、4a-b的符號。
如何判斷2a+b的符號?
看到2a和b,很容易聯想到拋物線的對稱軸-b/2a,事實上,透過判斷對稱軸-b/2a和1的大小,確實可以判斷出2a+b的符號。
例如,假設拋物線開口向上,則a>0,再假設對稱軸位於1的右邊,則-b/2a>1,變形可得-b>2a,則2a+b<0,是不是很簡單!
這種方法是判斷2a+b符號的最常用的方法。
同理,透過判斷對稱軸-b/2a與-1的大小,就可以判斷出2a-b的符號。
例如,已知a>0且-b/2a>-1,則-b>-2a,則2a+b>0。
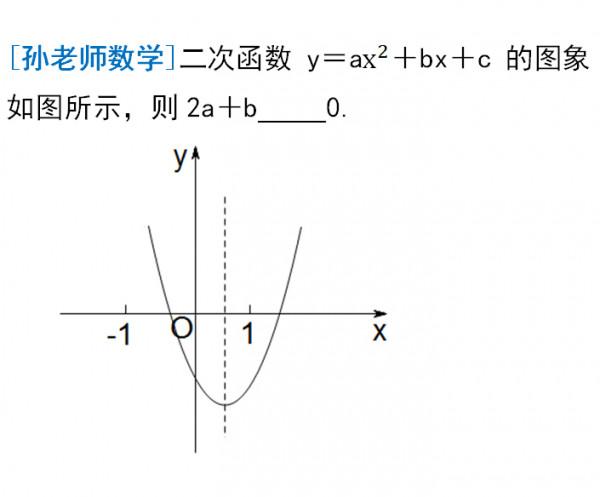
例1:
拋物線開口向上,所以a>0;拋物線的對稱軸在1的左邊,所以對稱軸x=-b/2a<1, 變形不等式即可得到2a+b的符號。
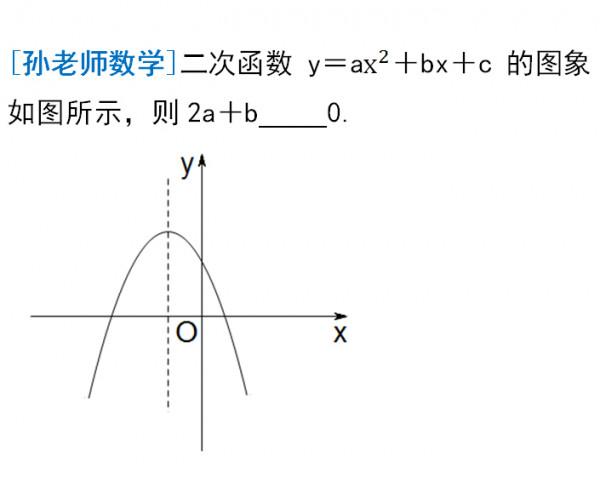
例2:
因為拋物線開口向下,所以a<0;對稱軸x=-b/2a位於y軸的左側,其為負數,所以-b/2a肯定小於1。
例3:
本題對稱軸在1的右邊,所以其大於1。
例4:
要比較2a和b的大小,只需判斷出2a-b的符號,則只需比較對稱軸x=-b/2a和-1的大小即可。
如何判斷4a+b和4a-b的符號?
和上面類似,要判斷4a+b的符號,只需判斷對稱軸x=-b/2a和2的大小;要判斷4a-b的符號,只需判斷對稱軸x=-b/2a和-2的大小。
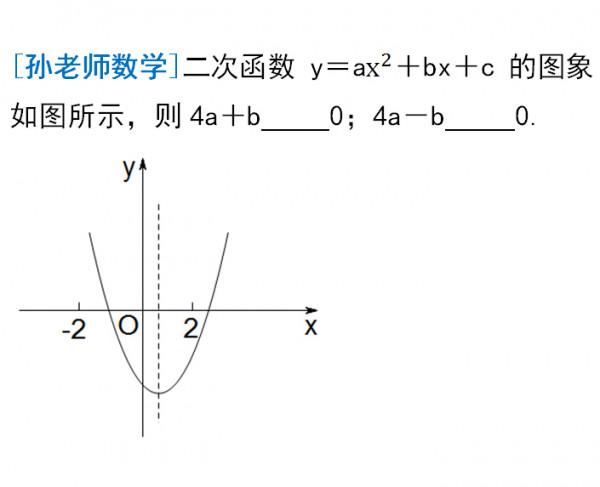
例5:
由圖可知,對稱軸在2的左邊,所以小於2;對稱軸在-2的右邊,所以大於-2。
加油!