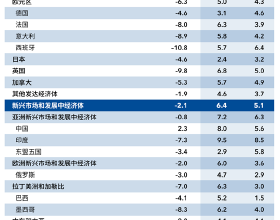
普拉納國家公園由幾條在交叉路口交匯的小徑組成。。每條小路的兩個端點都在兩個不同的路口,而每個路口正好是三條小路的端點。小路只在路口相交。最後,沒有小路在相同的兩個路口開始和結束。下面是一個可能的公園佈局的例子,其中有六個路口和九條小路。
一個遊客在公園裡的行走情況如下:她從一個路口開始,沿著一條小路行走。在第一條小路的盡頭,她進入了一個路口並向左轉。在下一個路口,她向右轉,以此類推,在每個路口交替進行左轉和右轉。她這樣做,直到她回到她開始的那個路口。在公園所有可能的佈局中,她在行走過程中進入任何路口的最大可能次數是多少?
這個問題的陳述非常冗長,但是我們有簡單圖(Simple Graph)工具可以幫助理解(預設為平面圖)。
簡單圖是指任意兩個頂點之間沒有超過一條邊,也沒有邊的起點和終點在同一個頂點的圖。換句話說,一個簡單的圖是一個沒有迴圈和多條邊的圖。
下面這個簡單圖中,每個頂點的度數為3(頂點的度數是指和該節點相關聯的邊的條數)。 讓我們看看根據題目要求的方式散步時,在每個頂點左右交替進行會發生什麼。
我在每條路徑上用字母 "L "和 "R "來表示散步者是左轉還是右轉。題目要求的是:進入任何路口的最大可能次數。在上面顯示的第一條路徑中,這個數字是1。
再選擇幾條路徑,我們發現有可能進入一個路口兩次。
為了考慮其他可能的行走方式,以更有規律的方向重新繪製圖形是有幫助的,這樣我們就可以看到對稱性。
一旦我們認識到這種對稱性,我們就可以看到,在這個公園裡沒有太多的 "不同 "路徑。透過不斷嘗試,我們發現不可能進入任何路口兩次以上。
但這個問題不僅僅是問所提供的公園的例子,而是問 "公園所有可能的佈局"。
我認為有兩個問題值得考慮。
- 對公園的可能佈局是否有限制,以幫助我們找到最大值?
- 為什麼會有一個最大值,也就是說,為什麼不可能在一個無限迴圈中不斷地進入同一個路口?
可能的公園佈局
從考慮最簡單的情況開始。給出的例子有6個路口(頂點),但是否有可能出現頂點更少的公園?我發現2個頂點是不可能的,因為 "沒有小路在同一個路口開始和結束",也就是說,這個圖形是 "簡單 "的。
我試著畫一個有3個路口的公園,但沒有成功,我意識到沒有奇數個路口是可行的。因為對於n個路口,邊的總數是3n÷2,(與每個頂點相連的3條邊,除以2以避免重複計算)。如果n是奇數,這個總數就不是一個整數。
有一個可能有4個路口的公園,但不可能多次進入一個路口。
例子中給出的是一個有6個路口的公園,我沒有找到具有6個路口的不同情況,所以我轉到了8個路口。
這個圖形是我熟悉的立方體的平面嵌入。它讓我意識到,所有符合給定條件的公園都可以表示為多面體。這是一個切入點。8個路口的公園不允許任何路口進入一次以上。
對於10個路口,遵循類似的結構,有一個內部和外部的五邊形。並嘗試了一些不同的走法,我發現有可能進入一個路口3次!
一個路口進入3次的例子
想出這個結構後,我覺得3可能是最大的可能。
另外,這時我已經意識到,可能的公園有無限的變化,為了解決問題,我不能輕易地進行分類。
- 可能的公園佈局情況
因此,我決定從我之前提出的關於無限迴圈的可能性的問題出發,重新審視這個問題。
排除無限迴圈的可能性
根據題意,散步者回到起點時將會停止。那麼,有沒有可能進入一個不包括起點的無限迴圈?這個無限迴圈會是什麼樣子呢?
在不失一般性的前提下,我們假設散步者進入了假設的無限迴圈,並向右轉。
這意味著他必須以左轉來結束這個迴圈,然後再右轉來重複這個迴圈。但由於她是從另一個方向來的,右轉會使她離開迴圈,如上面的動畫所示。
因此,我們已經表明,無論任何路口的最大入口數是多少,它至少是有限的!這就是我們的觀察。
關鍵觀察是,路徑是確定性的
一個重要的觀察結果是,一旦我們知道散步者是在某條小路(邊)上向左轉還是向右轉,接下來的每條小路就只有一種可能的選擇。同樣地,前一條小路也只有一種可能的選擇,以此類推。所以她的整個路徑是完全確定的。
我們也已經表明,不可能進入一個無限的迴圈,因為她回到起點後就停止了。所以不可能在一條特定的小路上左轉兩次,也不可能在一條特定的小路上右轉兩次。
這就把最大的可能上界減少到了6個(向左或向右轉入3條小路的每個路口)。
但它實際上有可能實現嗎?
當她進入一個路口左轉時,她必須右轉離開(反之亦然)。所以我應該在圖中加入出口。它將有6個箭頭進入,和6個箭頭出來。
總之,有些地方不對。為了走完所有這些路徑,她必須從她已經走過的路回來,但方向是相反的。
在下圖中,只包括了4個箭頭。橙色的箭頭表示她左轉進入路口,右轉出來,藍色的箭頭表示她後面需要走的相反方向。
為什麼這是不可能的?
正如我們之前所說,一旦我們知道路線和方向(左或右),整個路徑就完全確定了。特別是,一旦我們知道她沿著橙色箭頭左轉進入路口,我們就知道她的整個路徑形成了一個迴圈,從起點開始,在某個時間返回那裡。
為了沿著藍色箭頭行走,她需要走這個完全相同的迴圈,但方向相反。這是不可能的。一旦開始走這條路,就真的沒有回頭路了!這限制了可能的最大數量。
這個限制將一個路口的最大可能進入次數限制為3次。下面顯示了兩種可能性,根據進入-退出順序用顏色編碼。
我們已經展示了一個實現最大3次的公園的例子(上面的五邊形稜形結構)。
所以在公園所有可能的佈局中,3是她在行走過程中進入任何路口的最大可能次數。
圖論真了不起
圖論是離散數學的一個迷人的領域,有很多實際應用。特別是自從世界網路和社交媒體的出現。