雙層轉角雙層石墨烯的相關電子空穴態
文章出處:Peter Rickhaus, Folkert K. de Vries, Jihang Zhu, Elías Portoles, Giulia Zheng, Michele Masseroni, Annika Kurzmann, Takashi Taniguchi, Kenji Watanabe, Allan H. MacDonald, Thomas Ihn, Klaus Ensslin. Correlated electron-hole state in twisted double-bilayer graphene. Science 2021, 373, 1257-1260.
摘要:當兩片石墨烯之間的轉角接近1o時,石墨烯多層膜提供了一個瞭解電子相關物理性質的視窗。在這裡,作者報道了雙層轉角雙層石墨烯轉角為2.37°時相關電子空穴態的發現。在這個角度下,魔角狀態保留了大部分獨立的雙分子層特徵,允許雙分子層投射被門單獨控制。作者利用這一性質在狹窄的孤立電子和具有良好巢狀性質的空穴帶之間產生了能量重疊。作者的測量結果揭示了重構費米表面有序狀態的形成,與密度波態一致。這種狀態可以在不引入化學摻雜劑的情況下進行調節,從而可以研究相關的電子-空穴狀態及其與超導性的相互作用。
費米麵巢狀是指電子和空穴費米麵透過巢狀波向量Q平移而相互對映。由於巢狀意味著電子和空穴之間相干疊加的帶能成本很小,它有利於相互作用驅動的對稱破缺態。巢狀條件為ε(κF + Q) = -ε(κF),其中ε是一個很小的能量偏離費米能量,κF是費米波向量,說明如果兩個封閉的費米曲面完美巢狀,那麼它們包圍的面積是相同的。混合兩個由波向量Q巢狀的費米麵,得到波長為2π/Q的密度波(DW)階。在Peierls關於DW態的重要理論工作中,類自旋半填充帶之間發生巢狀,相互作用是晶格介導的,DW伴隨晶格畸變。電子間的庫侖相互作用也有利於DW態,在這種情況下,晶格畸變只起寄生作用,因此DW通常被稱為激子絕緣體。這一術語是由玻色子電子-空穴對態的凝聚而來的。在1T-TiSe2、Sb奈米片和高磁場下的雙量子阱中已經報道了平衡激子凝聚的證據。此外,在較大的層間偏壓作用下,在MoSe2/WSe2異質結構中,準平衡激子凝聚的研究取得了顯著進展。光泵浦電子空穴流體中非平衡激子和極化子的凝聚也得到了廣泛的研究。相關電子空穴態由於其豐富的內在物理特性以及與超導性的密切關係而不斷引起人們的關注。
轉角範德華材料,包括石墨烯雙層(轉角雙層石墨烯)和雙Bernal雙層[雙層轉角雙層石墨烯(TDBG)],是一種已被證實的設計魔角能帶的策略,有利於強化相關的電子態。在本研究中,作者尋求實現電子空穴帶都是巢狀的和相對狹窄的。為此,作者研究了TDBG在中間轉角下的性質,在中間轉角下,層耦合足夠強,可以形成魔角帶,但又足夠弱,可以保持解耦雙層的極化率。這個極化率可以用機率κt量化,以便於在頂層雙層的κt點(頂層雙層的Brillouin區角)處找到能帶狀態。如果機率κt很大,也就是在大的轉角下,應用位移場D將使頂部雙分子層充滿電子,底部雙分子層充滿空穴(圖1A)。但是相關的電子空穴態是脆弱的,即使它們發生,也只能被間接觀測到。因此,相關強度需要透過接近更小的角度來達到最大,其中變窄的魔角帶具有更大的有效質量m* (圖1B)。基於Bistrizer-MacDonald模型,作者討論了扭角和外場對機率κt和有效質量m*的影響,並將其推廣到TDBG的情況下。
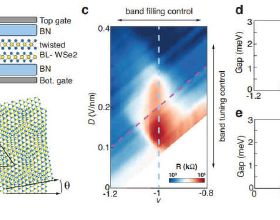
在這項研究中,作者表明相關的電子-空穴態更傾向於在中間轉角範圍內形成,大約在2o和3o之間。圖1C和D總結了θ = 2.37o時的主要實驗結果。作者觀察到在零總密度n =0,位移場D = 0.47 V/nm處有一個電阻峰(圖1C),當密度近似相同的電子和空穴同時存在時出現了電阻峰。這種共存在Landau fan測量中很明顯(圖1D),它揭示了能量交叉的電子和空穴迷你帶。
圖1
作者的裝置的側面示意圖如圖2A所示。作者透過對頂柵和背柵電極施加電壓Vt和Vb來調節密度n = (CtVt + CbVb)/e和位移場D = (CbVb - CtVt)/2ε0。這裡,Ct和Cb是對應的單位面積電容。圖1C中的電阻峰值是用圖2B中的接觸幾何圖形測量的。從電阻峰值隨溫度升高而降低的情況,利用阿累尼烏斯定律Rxx ∞ exp(Δ/2κBT)匯出了一個間隙Δ,其中κB為玻爾茲曼常數。在總密度n = 0時,Δ對D的依賴關係如圖2C所示。資料顯示D = 0 (灰色線)附近有一個間隙,隨著|D|的增加而關閉。另一個間隙在大的|D| (黃色線)處開啟。
為了確定間隙形成的條件,作者給出了不同n和D下的Shubnikov-de Haas (SdH)振盪的測量結果。在圖2D和E中,作者繪製了在垂直磁場B┴ = 1.5T中測量的反電阻∂/∂n (1/Rxx)的數值導數(選擇這個量是為了相關特徵的最佳可見性)。沿著圖2E中D = 0處的虛線,SdH振盪之間的間距對應一個頻帶簡併g = 8。透過改變D,簡併性得到提升,在深藍色和深紫色區域出現了帶有兩個斜率的SdH線(用箭頭表示)。在淺藍色和淺紫色區域,圖案發生變化,可以看到g = 4平行於n = 0這條線。在黃色區域SdH線的斜率再次發生變化,振盪變弱。
這些觀察結果表明在黑暗區域存在兩個子帶。它們的能量抵消被D調節,因此子帶與頂部和底部雙層相關。在淺藍色和淺紫色區域,只存在一個子帶,SdH振盪與D無關。由於位移場改變了子帶的能量偏移,包含兩個子帶的大D和小n(黃色區域)相對應的是電子-空穴流體,這與Landau fan圖1D中的斜率一致。重要的是,在n = 0和大D處觀察到的間隙出現在這個雙子帶區域的中間,因此強烈地表明它起源於電荷載流子相關性。區域邊界用一個基於拋物子帶的靜電模型很好地描述。實驗結果與圖2F到2H中不同相鄰層現場能量差ΔV在θ = 2.3°時的單粒子能帶結構一致。在ΔV = 0 (圖2f)時,在κt和κb點附近出現了四次自旋和谷簡併雙層石墨烯的兩個子帶,導致簡併度g = 8。改變ΔV (或D)打破了層簡併。對於有限的ΔV,出現g = 4的單帶區域(圖2G和H)。在電荷中性附近,有相反載流子型別的帶共存,帶隙閉合。與作者在圖2C中觀察到的兩個間隙相比,單粒子能帶結構(圖2F)僅捕捉到n = 0(能帶能量E = 0)和ΔV = 0處的間隙。這個間隙源於晶體場的組合,導致電子從外層轉移到內層和魔角晶格中的定域態。單粒子能帶結構在n = 0和有限的ΔV處沒有間隙,這與作者先前的建議一致,即該區域的實驗間隙來自電子-空穴關聯。
圖2
作者現在討論相關間隙對引數D和n的依賴關係,這些引數改變了電子空穴費米表面的大小。作者在圖3A中顯示了兩端電導G作為直流源漏偏置電壓Vsd的函式,並觀察到在n = 0和大D處的相干峰,表明了相干基態的形成。與熱啟用測量結果一致,間隙尺寸Δ隨D增大而增大。在D = 0.47 V/nm和n = 0時,Δ ≈ 5 meV (Δ由拐點決定)。作者注意到熱活化能和偏置間隙在這裡相差一個數量級。作者推測這是由於相關間隙的複雜熱擊穿造成的,並估計透過附加串聯電阻,偏差測量超出估計Δ約10%。在圖3B中,作者展示了Δ(n)在D = 0.47V/nm時的演變。當n ≈ 2.5 × 1011 cm-2時,間隙消失。
隨著|D|的減小和|n|的增大,相關電子-空穴能隙逐漸消失。第一個效應表明了有效質量和費米表面尺寸的重要性,兩者都隨著|D|的增大而增大,如圖3C所示。相反,|n|依賴表明,電子和空穴費米表面(藍色和紅色)之間的不對稱性增強削弱了間隙,如圖3D所示。一旦費米表面在尺寸上匹配(n = 0),就會出現相關狀態,並且間隙在較小的不對稱情況下會發生漂移,這強烈表明費米表面的巢狀(即二維輪廓)對相關狀態的形成起著至關重要的作用。
圖3
作者透過利用磁場改變費米表面來探索這個假設。圖4A描述了這種平行場測量的概念。在有限B‖時,能帶以塞曼能量位移。此時,在n = 0時,相對磁矩之間可能巢狀(等費米麵),而在n ≠ 0時,相同磁矩之間可能巢狀。實際上,測量的Rxx (n, B‖)軌跡與這個概念是一致的(圖4B)。在B‖ = 8T處可見有限n處的肩電阻,符合部分隙帶結構,其中一半載流子形成相關態,而其他磁矩帶保持導電。肩寬(n)隨塞曼能量增加。電阻增強區隨|B‖|和D的函式變化情況如圖4C。作者用一個基本模型來模擬對塞曼能量的依賴,得到圖4C中的虛線。
垂直磁場B┴的行為更為複雜。在圖4D中,作者展示了不同B┴的G (Vsd, D = 0.47 V/nm)軌跡。作者看到,間隙在臨界場Bc = 4T(橙色軌跡)處關閉,其Bc(D)依賴關係繪製在插圖中。在半經典的照片中,由於谷-塞曼效應,能帶會隨著B┴的變化而變化。雙層石墨烯gv值在~ 20至120範圍內的谷g因子在傳導帶和價帶中具有相反的符號。B┴因此在一個谷中增加電子和空穴密度,在另一個谷中降低,如圖4E所示。如果相關的電子空穴間隙是由波函式巢狀形成的,則其中一個谷的間隙(虛線帶-黃色間隙)隨著B┴的增加而增大,另一個谷的間隙(實線帶-紅色間隙)則減小。因此,帶結構的完全缺口部分隨著B┴的減少而減少,這與觀察結果一致。在這張圖中,B┴ > Bc的間隙可以解釋為K′處的單粒子間隙(圖4E中的綠色線)和K處的相關間隙,即谷極化相關態的形成。
圖4
磁場觀測結果與假設費米表面巢狀的基本模型一致。作者透過Hartree-Fock (HF)方法計算確認了電子空穴表面的巢狀,其中作者納入了庫侖勢並計算了相關的能隙Δ自洽。值得注意的是,魔角勢與新興的相關性無關,因為在相關能量範圍的中間轉角處,上下兩層之間的隧道作用很弱。透過HF方法的計算,作者得到了相關的波段。電子-空穴關聯打開了一個間隙,並隨相鄰層的現場能差ΔV而增大。間隙的大小和隨位移場的增大而增大的規律與實驗結果基本一致。作者指出,這種行為是隨著D降低靜態介電常數ε(q)的結果。
作者注意到,即使在n = 0時,同一谷中的費米麵(如κt和κb)也不是完美的圓形,這是由於中間的兩單分子層之間的層間隧道。然而,相反谷的費米麵(如κt和κ’b)是匹配的,這表明在n = 0時,相反谷的載流子形成了相關態。作者展示了計算出的費米曲面。
作者的模型允許作者調整每個雙分子層中二聚體位點之間的層間跳躍引數γ1來改變m*。有效質量m*通常取決於ΔV、中間層之間的層間跳躍引數ω、Bernal雙分子層內二聚體位點之間的跳躍引數γ1、轉角θ和費米速度νF。當ω ≠ 0時,改變ω、θ或ΔV會改變m*和層極化機率κt。當ω = 0時,改變θ或ΔV對m*沒有影響,而改變γ1或νF將使得m*對層極化沒有任何影響。為了研究m*單獨對相關間隙的影響,作者調整了每個雙分子層中二聚體位點之間的層間跳躍引數γ1。作者觀察到Δ(m*)幾乎呈線性增長,支援作者之前的說法,即m*決定了相關強度(圖1B)。理論計算結果顯示配對沒有對費米麵之間的動量差有很強的依賴性,只對有效質量有很強的依賴性。這與DW的激子特性一致。綜上所述,HF計算中的間隙開啟表明相關的電子-空穴狀態與DW一致。
相關的電子-空穴態可以看作激子絕緣體,並有望表現出逆流超流體。在沒有化學摻雜的情況下,可以透過改變n或在n = 0時改變D來控制DWs和無序態之間的量子相變,這種可調諧性為非費米液體物理提供了一個新的視窗。