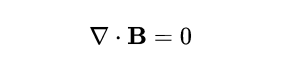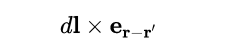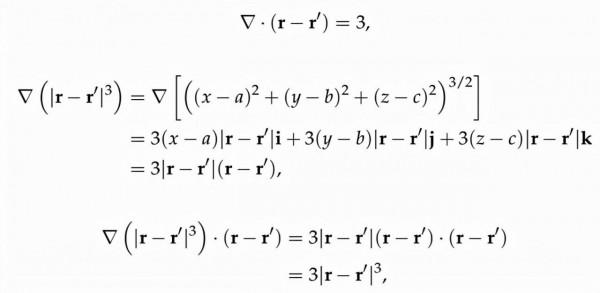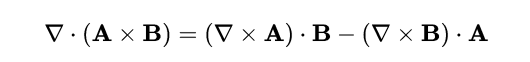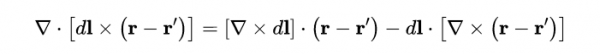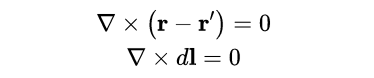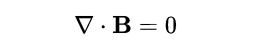麥克斯韋方程以一種相當優雅和數學上緊湊的方式描述了電和磁的相互作用。在這些方程中，高斯的磁定律對於理解電磁波和導電介質之間的相互作用極為重要。但是，這個定律往往被寫成簡單的形式：

• 式1

它否認了自然界中磁單極的存在。當涉及到電荷時，我們通常可以認為它們是正的或負的。在這個意義上，當我們把某一空間的所有電荷加起來時，最後總是可以得到一個淨電荷或者是零（中性電荷）。磁學的情況則不然。磁鐵總是有兩個極，北極和南極。即使把一塊條形磁鐵切成兩半：也不會得到兩個 "單極"。相反，你會得到兩個較小的條形磁鐵，每個都有自己的南北兩極。因此，當你試圖測量透過任何表面的淨磁通量時，總是得到零：這意味著不可能存在磁單極，否則磁通量就會是零以外的數值。

儘管這個小方程很重要，但物理學和工程學的學生往往不知道這個方程是如何形成的，或者說它在數學上是如何實現的。在這篇文章中，我將向你介紹得出這一不可思議結果的步驟。

畢奧-薩伐爾定律（The Biot-Savart law）

為了開始討論如何得出公式（1），我們必須首先了解磁場是如何形成的。從幾個世紀前的一個小經驗觀察開始：所有的磁場都是移動電荷的結果。在這個意義上，物體中的每一個原子都擁有自己的磁場，這是由於電子圍繞其原子核的運動造成的，但其方向隨著時間的推移變化得非常快。

為了充分解釋材料中的磁性現象，我們需要研究統計力學（這已經超出了本文的範圍）。現在，我們將專注於宏觀尺度的磁場。讓我們從一個基本的觀察開始：任何電流I = dq/dt都是由電子沿著導電材料的運動產生的。如果我們抓起一根寬度可以忽略不計的電線，並以任意的方式在空間中形成一個圍繞中心參考點（例如原點）的環形，那麼電流I將總是流向一個方向：電線本身的切線方向。然後，讓我們定義一個無限小的導線元素dl，在每一點上都以切線為方向。根據實驗證據，運動的電流會產生一個垂直於其運動方向的磁場（因此有一個叫作右手規則的東西）。考慮到這一事實，以及電流引起的磁場強度的經驗公式I：

• 式2

其中r是與電流源（導線）的距離。我們現在透過考慮導線dl的每個元素的貢獻來建立一個總磁場。為此，我們考慮到每一點的磁場方向，這是由導線的切向分量和位置向量之間的叉積給出的。

其中

是沿r-r'指向的單位向量。這裡，r是相對於座標系的位移向量，而r'是導線上每一點的無限小元素dl的位置。最後，把所有這些表示式放在一起，可以得到：

• 式3

現在將這個方程的兩邊在導線的整個長度上進行積分，可以得到磁場的表示式：

• 式4

這通常被稱為畢奧-薩伐爾定律。這將是我們推導高斯磁定律的起點。

從畢奧-薩伐爾定律推匯出高斯的磁定律

現在我們已經介紹了磁場作為空間位置函式的一個主要表示式，我們可以考慮在空間中每一點的場的散度會發生什麼。首先，我們將定義幾個非常重要的向量微積分特性，即：

• 方程5 (a) - (c)

這使得我們可以寫出：

• 式6

此外，我們還推匯出以下表達式：

此外，利用標量三重積特性（scalar triple-product identity）：

• 式7

我們得出的結果是：

在這一點上，我們可以考慮到以下事實：

與=0，因為我們是在取一個向量與自身的叉積，所以我們得出結論：

另一方面，我們發現以下關係成立

透過一些基本的計算，我們很容易發現以下兩個結果是真的

最後，簡化所有這些項，我們可以得出磁場散度的結果：

• 式7：高斯磁定律的微分形式

被稱為磁場的高斯定律。這意味著什麼並不明顯，但是應用發散定理

• 式8：高斯磁定律的積分形式

我們可以看到，透過一個任意表面的總磁通量必須正好為零。由此我們推斷，一定沒有磁單極存在，因為首先就沒有磁通量可供測量。相反，我們只能測量單個磁偶極周圍的磁通量，由於對立的兩極，它總是零。