維度的概念乍一看似乎很直觀。瞥一眼窗外，我們可能會看到落在纖細的旗杆上體驗零維空間的烏鴉，被限制在一維電話線上的知更鳥，在二維地面上自由移動的鴿子，還有翱翔在三維空間的老鷹。

但是對於數學家來說，為維度的概念找到一個明確定義實則異常困難。我們經過數百年的思想實驗和富有想象力的比較，才得出目前對維度概念的嚴格理解。

1. 超越三維

古人知道我們生活在三個維度中。亞里士多德[1]寫道：“向一個方向延伸的是直線，兩個方向延伸的是平面，三個方向延伸的是物體。除此之外就沒有其他了，這些就是所有的維度。”

然而相比於其他人，數學家更熱衷於想象更多維度的思維訓練：垂直於已知的三個維度的第四維度會是什麼樣子？

一種流行的方法：假設我們的可知宇宙是三維空間中的二維平面。一個在平面上方的實心球對我們來說是看不見的。但是如果它墜落並接觸到平面，就會出現一個點。當它繼續穿過平面時，圓盤會不斷變大，直到達到其最大尺寸，然後縮小並消失。正是透過這些橫截面，我們才能看到三維物體的形狀。

圖1：在平面上只能看到三維物體的橫截面。| 來源：Samuel Velasco/Quanta Magazine

類似地，在我們熟悉的三維宇宙中，如果一個四維球穿過它，這個四維球會以一個點的形式出現，之後成為一個實心球，最終達到完整半徑的球，然後半徑減小並消失。這給了我們關於四維形狀的感知，但是對於這樣的物體，還有其他思考方式。

例如，讓我們嘗試透過構建超立方體來視覺化立方體的四維等價物。如果我們從一個點開始，可以在一個方向上拖動它以獲得一條線段。之後，當我們垂直於拖動方向移動線段時，得到一個正方形。在第三個垂直方向拖動這個正方形會產生一個立方體。同樣，我們透過在第四個方向上拖動立方體來獲得超立方體。

圖2：透過將藍色位置的圖形拖動到紫色位置，我們可以視覺化各種維度的圖形，包括超立方體。

或者，就像我們可以將立方體的面展開為六個正方形一樣，我們可以展開超立方體的三維邊界以獲得八個立方體，正如薩爾瓦多·達利 (Salvador Dalí) 在 1954 年的畫作《受難》(Crucifixion，Corpus Hypercubus) 中所展示的那樣。

圖3：我們可以透過展開正方體得到的面來想象一個立方體。同樣，我們可以透過展開超立方體得到的立方體來想象超立方體。

所有這一切構成了對維度的直觀理解，即如果一個抽象空間有n個自由度（就像本文開頭提到的那些鳥一樣），或者需要n個座標來描述一個點的位置，該空間就是n維的。然而，數學家發現維度比這些簡單的描述要複雜。

2. 定義維度

人們對更高維度的正式研究出現在19世紀，相關研究在幾十年內變得相當複雜：1911年的參考書目包含1832條對n維幾何的引用。也許因此，在19世紀末和20世紀初，公眾開始迷戀第四維度。1884 年，埃德溫·阿博特 (Edwin Abbott) 創作了流行的諷刺小說《平面國》（Flatland），小說以二維生物遇到三維生物作為類比，幫助讀者理解第四維度。1909 年《科學美國人》徵文比賽題為“什麼是第四維？” ，有245份參賽作品爭奪500美元的獎金。許多藝術家，如巴勃羅·畢加索（Pablo Picasso）和馬塞爾·杜尚（Marcel Duchamp），將第四維的想法融入到作品中。

但在這段時間裡，數學家們意識到，維度缺乏正式的定義實際上是一個問題。

喬治·康托爾 (Georg Cantor) 因發現無窮大有不同的勢 (cardinality）而聞名[2]。起初，康托爾認為線段、正方形和立方體中的點集必須具有不同的勢，就像一條10個點的線、一個10×10的點網格和一個10×10×10的點立方體有不同數量的點。然而，在1877年，他發現線段中的點與正方形（以及所有維度的立方體）中的點之間存在一一對應關係，這表明它們具有相同的勢。憑藉直覺，他證明了儘管維度不同，線、正方形和立方體都具有相同數量的無窮小的點。康托爾寫信給理查德·戴德金（Richard Dedekind），“我看到了，但我不相信它。”

康托爾意識到這一發現威脅到n維空間需要n個座標來描述的直覺觀念，因為n維立方體中的每個點都可以由一段區間中的一個數字唯一標識。因此，從某種意義上說，這些高維立方體相當於一維線段。然而，正如戴德金指出的那樣，康托爾的函式是極不連續的——它本質上是將一條線段分成無限多個部分，然後將它們重新組合成一個立方體。這不是我們所希望的座標系的行為。這種座標系太過無序，無法為我們描述物體提供幫助，就像是為曼哈頓的建築物提供唯一地址卻隨機分配這些地址。

然後，在1890年，朱塞佩·皮亞諾 (Giuseppe Peano) 發現，可以將一維曲線纏繞得如此緊密且連續，以至於可以填充二維正方形中的每個點。這是第一條空間填充曲線（space-filling curve）。但皮亞諾給出的例子也不是座標系的良好基礎，因為曲線與自身無限多次相交。回到對曼哈頓的比喻，這就像給一些建築物多個地址。

圖4：這些是產生空間填充曲線的前五個步驟。在每一步，曲線的面積為零，但在極限情況下，它填充了正方形。這條特殊的曲線是由大衛·希爾伯特（David Hilbert）引入的。

這些和其他令人驚訝的例子清楚地表明，數學家需要證明維度是一個真實的概念。例如，當n≠ m時，n維和m維歐幾里得空間的某些基本性質是不同的。這個目標被稱為“維度不變性”（invariance of dimension）問題。

終於，在1912年，在康托爾的發現之後將近半個世紀，在人們多次證明維數不變性的嘗試失敗之後，布勞威爾（L.E.J. Brouwer）使用自己創造的一些方法並取得了成功。從本質上講，他證明了不可能將一個更高維的物體放入較低維度的空間中，以及在不將物體分成許多部分（如康托爾所做的那樣）、不允許物體與自身相交（如皮亞諾所做的那樣）的情況下，使用較低維度的物體填滿較高維度的空間。此外，大約在這個時候，布勞威爾等人給出了各種嚴格的定義，例如，可以根據球在n維空間中的邊界是n-1維這一事實，幫助歸納地確定維數。

儘管布勞威爾的工作將維度概念置於強大的數學基礎上，但它無助於增強我們對高維空間的直覺：對3維空間的熟悉太容易使我們誤入歧途。正如托馬斯·班喬夫 (Thomas Banchoff) 所寫，“我們所有人都是對自己所在維度存有偏愛的奴隸。”

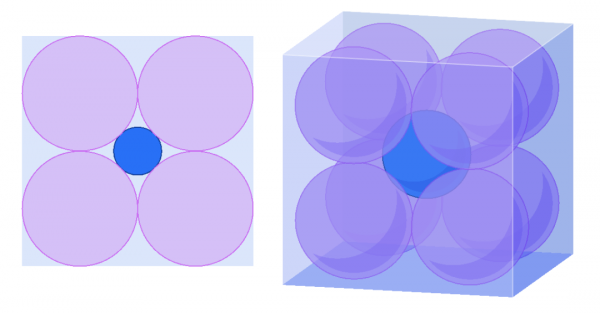
例如，假設我們將2n個半徑為1的球體放置在邊長為4的n維立方體中，然後將另一個球體放置在與它們中心相切的位置。隨著n增加，中心球體的大小隨之增加——它的半徑為√n -1。但是，令人震驚的是，當n≥10時，這個球體會伸出立方體的邊。

圖5：中心球體隨著維度的增加而變大，最終會突出到立方體外面。

高維空間中令人驚訝的現實導致統計和資料分析出現問題，統稱為“維數災難”（curse of dimensionality）。許多統計方法所需的樣本點數量隨維度增加呈指數增長。此外，隨著維度增加，點形成聚類的機率會降低。因此，找到為高維資料降維的方法十分重要。

3. 分形和非整數維度

維度的故事並沒有因為布勞威爾而終結。僅僅幾年之後，費利克斯·豪斯多夫（Felix Hausdorff）提出了一個新的維度定義，之後的數學發展證明該定義對現代數學至關重要。

考慮維度的一種直觀方式是，如果我們將d維物體均勻地縮放或放大k倍，它的大小會增加到kd倍。假設我們將一個點、一條線段、一個正方形和一個立方體放大3倍，點的尺寸不變（30=1），線段變成3倍（31=3），正方形變成9倍 (32=9)，立方體變成27倍 (33=27)。

圖6：當我們將d維物件放大k倍，其尺寸會增加到 kd 倍。

豪斯多夫定義的一個令人驚訝的結果是，物體可能具有非整數維度。幾十年後，當伯努瓦·曼德爾布羅特（Benoit B. Mandelbrot）問道：“不列顛的海岸有多長？”時，結果證明非整數維度正是他所需要的。海岸線如此參差不齊，以至於無法用任何尺子精確測量——尺子越短，測量結果越大越精確。曼德爾布羅特認為，豪斯多夫維數提供了一種量化這種鋸齒狀海岸線的方法，並在 1975 年提出了術語“分形”來描述這種無限複雜的形狀。

圖7：英國海岸線的測量長度取決於尺子的大小。

要了解非整數維度可能是什麼樣子，讓我們考慮以迭代方式生成的科赫曲線（Koch curve）。我們從線段開始。在每個階段，我們刪除每個線段的中間三分之一，並用與刪除的線段長度相等的兩個線段替換它，無限次地重複此過程以獲得科赫曲線。仔細研究它，你會發現它包含4個與整個曲線相同但大小隻有三分之一的部分。因此，如果我們將這條曲線縮放3倍，我們將獲得原始曲線的4個副本。這意味著其豪斯多夫維數d滿足 3d=4，因此，d=log3(4)≈1.26。科赫曲線並不像皮亞諾曲線那樣完全充滿空間，所以它不是二維的，但它也不是一條一維線，而是1.26 維。

圖8：科赫曲線包含四個與整條曲線相同但尺寸為其三分之一的部分，因此其豪斯多夫維數不是整數，而是 log3(4)≈1.26 維。

4. 四維時空之外

最後，有些讀者可能會想，“時間不是第四維嗎？” 事實上，正如威爾斯1895年的小說《時間機器》（The Time Machine）中的發明者所說：“時間與空間的三個維度中的任何一個都沒有區別，只是我們的意識沿著它移動。” 1919 年，作為第四維的時間在公眾的想象中爆發，日食讓科學家們證實了愛因斯坦的廣義相對論和閔可夫斯基（Hermann Minkowski）的平坦四維時空的曲率。正如閔可夫斯基在1908年的一次演講中所預言的那樣，“此後獨自的空間和獨自的時間註定會消失在陰影中，只有空間和時間的某種結合才能保持獨立的現實。”

今天，數學家和其他人的研究經常偏離我們所在的三個維度。有時研究會涉及額外的物理維度，例如弦論所要求的那些維度，但更多時候我們抽象地工作，並不設想實際空間。一些研究是幾何的，例如瑪麗娜·維亞佐夫斯卡（Maryna Viazovska）在2016年發現了在8維和24維填充球體的最有效方法[3]。在物理、生物學、工程、金融和影象等不同領域研究分形時，有時需要非整數維度。在這個“大資料”[4]時代，科學家、政府和企業建立了人、地點和事物的高維度檔案。

幸運的是，無論鳥類和數學家，都不需要完全理解維度就可以體驗維度。

原文：

https://www.quantamagazine.org/a-mathematicians-guided-tour-through-high-dimensions-20210913/

參考連結：

[1]https://www.sciencedirect.com/topics/mathematics/euclid

[2]https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/

[3]https://www.quantamagazine.org/sphere-packing-solved-in-higher-dimensions-20160330/

[4]https://www.quantamagazine.org/tag/big-data

來源：集智俱樂部

編輯：Eric、yrLewis