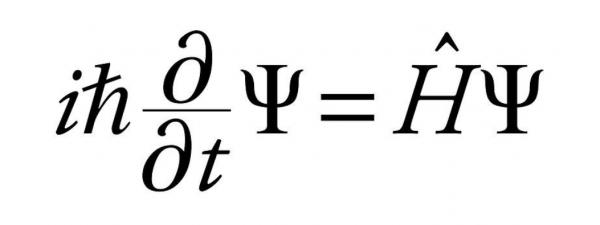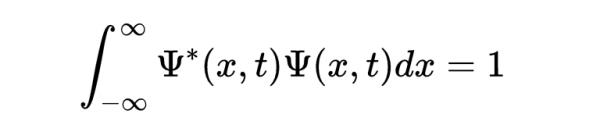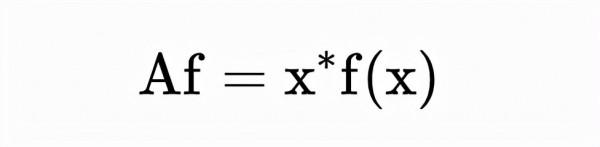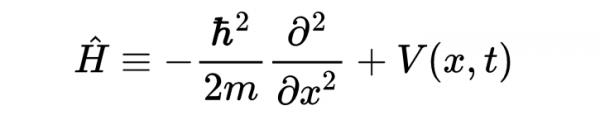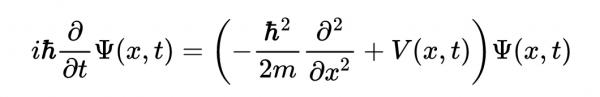量子力學無處不在，從地球上的最小角落到太陽的核聚變，這一基本的物理學理論在我們理解宇宙的發展過程中起到了非常重要的作用。量子力學中交織著許多了不起的定理，但其皇冠上的明珠無疑是薛定諤方程。雖然它乍一看很複雜，但我們將在本文中解析它，它實際上是相當簡單的，每個人都可以理解。

量子力學

量子力學的主要目的是在原子和亞原子粒子的尺度上對物體的物理特性提供準確的描述。在其發展之前，每個人都期望這種尺度的粒子的行為能用經典力學解釋。然而，令所有人驚訝的是，不僅不是這樣，量子世界遠比我們想象的要奇怪。

事實證明，亞原子粒子的領域在本質上是非確定性的。這意味著，我們永遠無法確定一個亞原子粒子的位置，或任何其他物理屬性。亞原子世界是由機率決定的。這在當時是一個很大的啟示。我們的宇宙在基本層面上不是確定的，這一事實不僅在物理學上，而且在哲學上都引起了爭論的爆發。

波函式

薛定諤方程是由埃爾文-薛定諤在1926年提出的，內容如下：

一些熟悉高等數學的人可能會認出上面的一些或全部符號。

上述方程中表達的內容有很多，但有一點很突出，就是希臘字母Ψ。這就是通常用來表示波函式的符號。但什麼是波函式？

所有物理學中最為重大的發現之一是波粒二象性，它表明，所有的物質都有波的性質和粒子的性質。這並不意味著一個粒子，也是一個波。然而，在某些情況下，其行為最好用通常用於描述波的函式來描述。

• 薛定諤

亞原子粒子具有一些波的特徵。但波函式究竟描述了什麼？這是有趣的部分，也是量子力學起初難以理解的原因。馬克斯·玻恩在1926年提出了這個關鍵的假設。

在某一點找到一個粒子的機率密度，在測量時，與該點的粒子波函式的大小的平方成正比。

讓我們把它分解一下。

在薛定諤方程中出現的波函式，在本質上是一個複數函式，以時間t和三個空間座標x、y、z作為其引數。複函式是說它在給定輸入值時能產生複數的函式。因此，作為一個複函式，一開始確實很難想出一個適用於現實世界的解釋。我們知道它不能描述粒子的位置或加速度，例如，因為如果它描述了，它就會是一個實數函式。

但後來，馬克斯-博恩提出了一個想法：也許波函式與機率有關。但機率是實數，因此，他認為我們可以取其幅度的平方（每個複數和函式都有一個振幅）來獲得一個實值，而不是直接將其值與機率聯絡起來。玻恩是正確的。

• 一個具有動量p和能量E的粒子的波函式或德布羅意波

讓我們回顧一下到目前為止我們所說的內容。

亞原子粒子的行為與經典物體不同。它們既擁有類似波的特性，也擁有類似粒子的特性。此外，描述這種大小的粒子的方程在本質上是機率性的。薛定諤方程中的波函式是一個函式，其在空間和時間的某一點的值與粒子當時在那裡的機率有關。它是如何相關的呢？它的大小的平方是機率密度（也就是每單位體積的機率），我們在空間的某個位置找到粒子的機率。

所以這就是波函式所表達的。上過機率課程的人可以預見到它的一些特性。首先，我們對歸一化的波函式感興趣。

• 波函式的歸一化 。為了簡單起見，這是一個一維（x維）的波函式

如果我們想一想，這是很直觀的。由於波函式大小的平方（等於我們在積分裡面看到的波函式與其共軛物的乘積）給出了機率密度，那麼我們要求總的機率是1。

我們已經“破譯”了波函式背後的奧秘。現在讓我們深入研究薛定諤方程。

薛定諤方程

記住我們到目前為止所說的一切，薛定諤方程描述了機率波的形式，它們是如何隨時間演變的，以及它們在外部影響下的行為。讓我們把它一點一點地分解。

從左手邊開始，我們首先遇到的兩個符號是 "i"（虛數單位）和 "h"（普朗克常數）。儘管這些數字（符號）本身非常重要，但它們對於理解薛定諤方程並不重要，因此，我們在本文中不會涉及它們。

我們遇到的下一個表達是波函式的時間導數。時間導數本質上是告訴我們某些東西相對於時間的變化速度。在這種情況下，是波函式的變化有多快。

H上面加個“帽子”被稱為哈密爾頓運算元。對於那些不熟悉這個概念的人來說，簡單地說，運算元是一個函式，它的輸入不是一個數字，而是另一個函式本身！它們將一個函式轉換成另一個函式。例如，我們可以將運算子A定義為任意給定函式f = f(x)並將其乘以x的運算元：

哈密頓運算元的公式稍微複雜一些。

• 哈密頓運算元

它一開始看起來很嚇人，但它實際上是相當簡單的。透過代入運算元來寫薛定諤方程，我們可以得到：

• 薛定諤方程。

你要理解的不是數學符號，而是哈密爾頓運算元的本質。

哈密頓運算元與我們系統中的動能和勢能有關。

勢能部分應該很清楚。上述總和中的第二項實際上是V(x,t)，它是施加在系統上的外部勢能。不明顯的是動能。事實證明，和中的第一項本身就是量子力學中的一個運算元，它與特定狀態的動能有關。

這裡有很多細微的差別，但這並不重要。你所要記住的是，哈密爾頓運算元與系統的總能量有關。重要的事再說兩遍：

哈密爾頓運算元與系統的總能量有關。

哈密爾頓運算元與系統的總能量有關！

薛定諤方程告訴我們，波函式或量子態正在隨著時間的變化而變化。它的變化方式取決於系統的總能量（勢能+動能）。

結論

薛定諤方程是所有物理學中最著名的方程之一。它使我們能夠對各種量子系統以及它們如何隨時間演變做出準確的預測。然而，它的應用也有一些限制。事實證明，對於包含眾多粒子的系統來說，即使是用最強大的計算機，要解薛定諤方程也是非常困難的。很多專家希望，當我們發明了量子計算機後，這一限制將被解除，但就目前而言，這一優雅的方程並不適合描述大規模的量子系統。

想了解更多精彩內容，快來關注老胡說科學