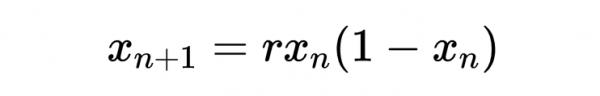我第一次接觸混沌理論是透過《侏羅紀公園》中的馬爾科姆教授這個角色。作者將混沌理論描述為一種潛在的數學結構。

混沌理論是 "蝴蝶效應 "的原因。一隻蝴蝶在中國拍打翅膀，而紐約市卻因此下雨了，因為扇動翅膀會引起能量由小到大的級聯。不過，你不需要在中國觀察蝴蝶，並將其與紐約的天氣統計聯絡起來，就能理解混沌。只需要一個鐘擺。

混沌系統有一種叫做 "對初始條件的敏感依賴 "的東西。這意味著，不僅中國的一隻蝴蝶可能導致紐約下雨，而且如果你重複這個實驗，永遠不會得到相同的結果。對於科學家來說，這是一個能夠精確預測未來的理論障礙，即使沒有量子力學的測不準原理。

讓我們看一個例子。以一個鐘擺為例，用兩個量來描述它在任何時候的狀態：位置（由其沿擺動方向的位置給出）和動量（其質量和速度的乘積）。如果把這兩個值畫在一個網格上，位置在橫軸上，動量在縱軸上，在一系列的時間裡，你會看到鐘擺描出一條線。這個網格被稱為鐘擺的相空間。這條線是它的相空間軌跡。

假設鐘擺的開始位置和動量為（x，p），在網格上記錄了它的運動軌跡。現在，從一個不同的位置開始（x+δ，p+ε）。新的軌跡將與舊的軌跡發生偏離。然而，對於一個非混沌擺來說，它要麼收斂，要麼保持非常接近。這就是對初始條件的敏感依賴性。

然而，這種差異在許多情況下並不是指數級的，因為混沌系統有所謂的奇異吸引子，也就是一組初始條件，稱為吸引力盆地（a basin of attraction），被吸引到相空間的一個特定區域。這意味著，一個混沌擺，當在一個吸引盆地中開始時，將趨向於一個類似於從盆地中其他點的軌跡，但永遠不會是相同的軌跡。

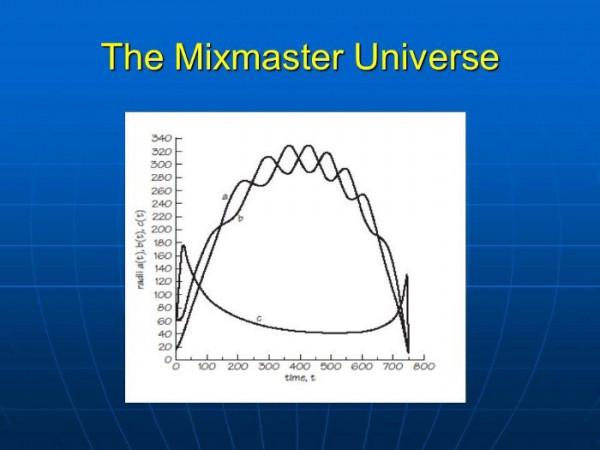
Mixmaster宇宙（MM宇宙）

Mixmaster宇宙是查爾斯-米斯納（Charles Misner）在20世紀60年代提出的早期宇模型。Mixmaster宇宙是同質的，這意味著，像大多數宇宙學模型一樣，它假定整個宇宙的物質密度是相同的。然而，它不是一個各向同性的宇宙，而是各向異性的，意味著宇宙在不同的方向上可能表現得不同。你可以把球體看作是一個各向同性的固體，而橢圓體或扁球形是各向異性的。

Mixmaster宇宙以Sunbeam Mixmaster命名，Sunbeam是Sunbeam Products的一個品牌，電動廚房攪拌機

根據我們的觀察，我們的宇宙是同質的並且是各向異性的。因此，Mixmaster宇宙（如果存在），必須是非常早期的宇宙。宇宙開始時應該是各向異性的，並迅速收斂到各向同性的形式。

Mixmaster宇宙是一個混沌的宇宙。它在一個方向上反覆膨脹和收縮，同時在另一個方向上膨脹，然後這些方向互換位置。因此，它的行為就像一個三維混合器，反覆而隨機地擠壓和膨脹。

米斯納認為Mixmaster宇宙可以解釋為什麼宇宙微波背景(CMB)混合得如此之好。這不可能是普通的電磁力或其他力導致的。天體物理學家現在認為，是膨脹造成了混沌。 mixmaster宇宙是愛因斯坦方程的唯一解，已被證明是混沌的。

雖然混沌是一個很容易理解的概念，但它是出了名的難以證明。我們所知的大多數混沌系統都是一維或二維的，證明多維繫統混沌的標準方法實際上是將其簡化為一維問題。因此，證明一個四維宇宙學是混沌的是一個艱鉅的任務。

但首先，混沌（ chaos）與混合有（mixing）什麼關係？

在19世紀，科學家們試圖瞭解物質如何混合的數學原理，在什麼條件下可以認為是混合，以及什麼過程導致混合。他們發現了四個層次的混合：遍歷混合（ergodic）、弱混合（weakly mixed）、強混合（strongly mixed）和伯努利移位（Bernoulli shifted）。

假設你正在製作雞尾酒，有10%的朗姆酒和90%的可樂。你可以製作一種混合方式的雞尾酒。

• 遍歷混合的雞尾酒是混合得最不均勻的，如果你取任意體積的朗姆酒和可樂，隨著時間的推移，朗姆酒的平均含量是10%。這意味著在任何特定時間朗姆酒的比例可能是任何值。
• 對於混合程度較弱的雞尾酒來說，除了偶爾有一次，體積中有10%的朗姆酒。
• 對於烈混合的雞尾酒，朗姆酒的比例始終是10%。
• 伯努利移位的雞尾酒不僅總是10%的朗姆酒，而且雞尾酒的“結構”在每一時刻都是完全隨機的，你可以把它看作是一種不僅混合良好，而且處於不斷攪拌狀態的雞尾酒。

伯努利移位混合也被稱為phi-混合，是一種特殊的混合，因為它是偽隨機的。它可以用於偽隨機數生成器，並可能是布朗運動的原因。許多混沌系統表現出這種混合，包括Mixmaster宇宙。

讓我們看一些混沌系統的例子。

理解混沌系統的最簡單方法是使用所謂的對映，這只是系統狀態x在時間n和時間n+1之間的關係。如果它是一個一維繫統，那麼x只是一個數字。

邏輯斯諦對映（The logistic map）是最古老的混沌對映之一，模擬人口的增長和崩潰。邏輯斯諦對映並不總是混沌的。相反，它可能是也可能不是，取決於一個可控引數的大小。

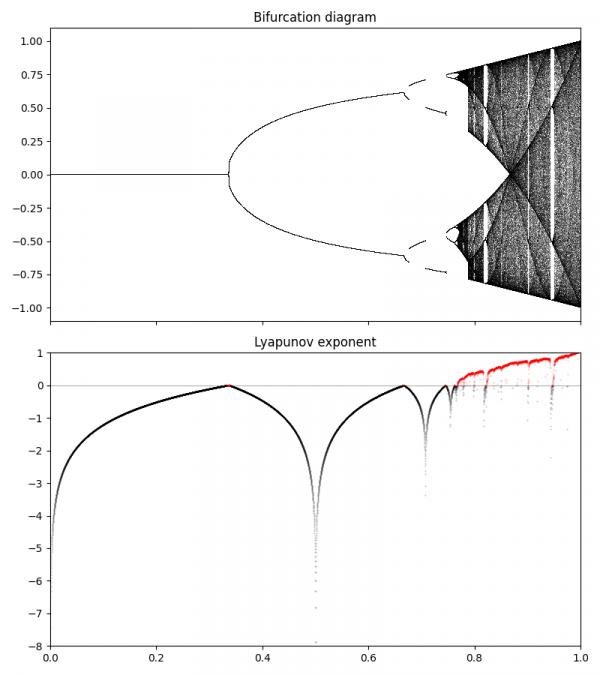
這裡的可控引數是r，唯一能控制的是它的起始位置。如果讓這個對映執行一段時間（用一點Python程式碼就可以輕鬆搞定），它將趨向於收斂到一個或兩個或更多的點，或者完全隨機。你可以把所有這些收斂點收集到一個叫做分叉圖的圖中。我透過對10000個r值的地圖進行1000次迭代，並對每個r值的最後100次迭代進行繪製，建立了一個分叉圖。

你可以透過看圖知道它在哪裡變得混沌。這100個值在圖上到處都是。但用數學的方法來看，就是計算李亞普諾夫指數，這是衡量其相空間中兩個相鄰軌跡發散的速度。如果這個指數是負的或者是零，這意味著系統收斂到一個特定的狀態叫做不動點或者變成周期性的，那它就不是混沌的。如果它是正的，它就是混沌的。

這裡的一個有趣的特點是，你可以看到在走向混沌的過程中，狀態會經歷一個叫做 "週期加倍 "的東西。一開始是小的r，小於3，收斂到一個單一的固定點。在那之後，它在兩個狀態之間徘徊。然後它再次翻倍到4。每次翻倍，李亞普諾夫指數都達到零，與混沌接近，然後在上升之前再次下降。你看不出來，但週期繼續翻倍2、4、8、16、32，但是在r的範圍內，它們每一週期花費的時間變短了。然後你可以看到，在r=3.57左右，它變得混沌。仍有一些短暫的時期，它又回到了非混沌狀態。你可以在隨機性之間看到那些白條。

另一個例子是切比雪夫多項式（ Chebyshev polynomials）。有無數個這樣的例子，它們都具有很強的混沌性。

這裡是一個三階切比雪夫：

這些地圖很混沌，它們可以代替完全隨機的噪音。

切比雪夫多項式也被用於密碼學中，因為它們不可預測，但對0非常對稱。

現在，讓我們來談談Mixmaster宇宙中的混沌情況。

Mixmaster引入了三個比例因子，a、b和c，每個空間方向都有一個。因為它們是同質的，所以它們隨時間變化，但不隨空間變化。另一方面，因為它們都可以是不同的值，所以宇宙不是各向同性的。

你可以將下面的Mixmaster宇宙與標準宇宙，即FLRW宇宙進行比較，後者只有三個方向的一個比例因子。

• 兩個比例因子振盪，而一個收縮和膨脹。(約翰-D-巴羅)

• FLRW宇宙學（維基媒體）

為了證明Mixmaster宇宙是混沌的，你必須把它還原成一個一維對映。愛因斯坦方程保證了其中一個比例因子，比如說c，取決於另外兩個，a和b，所以它已經是二維的了。

在這種情況下，兩個維度仍然太多，我們可以使用一個數學技巧將其進一步減少到一個維度，這個數學技巧被稱為龐加萊迴歸對映。一些二維或更多維的空間，那麼你該空間的軌跡必須透過它的一個橫截面。

如果迴歸對映是混沌的，那麼高維一定也是混沌的。我們可以證明，該對映對於Mixmaster是混沌的。

• 龐加萊地圖。

不幸的是，在愛因斯坦的宇宙中，這還不夠，因為我們總是可以選擇新的座標系，我們怎麼能知道沒有一個座標系可以完全消除混沌的呢？尤其是李亞普諾夫指數，是依賴於座標的，所以在這種情況下作為混沌的指標是不可靠的。

在90年代末，人們設計了一種與座標無關的分形方法，並表明米斯納的宇宙確實是混沌的。

這種分形方法（而不是研究對初始條件的敏感依賴），表明Mixmaster宇宙的動力學包含一個奇怪的排斥物，它類似於一個奇怪的吸引子，但具有排斥性，因為系統傾向於遠離它而不是流向它。這有點像球滾向山頂而不是山谷。

趨向於被一個特定的吸引子吸引或被一個排斥子排斥的一組初始條件被稱為它的吸引盆地或排斥盆地。如果該盆地有一個邊界是分形的，那麼你就知道它是一個奇怪的吸引子或排斥子，系統是混沌的。

例如，二維繫統：

有一個分形盆地邊界，你可以在所有的峰上看到：

Mixmaster宇宙有一個類似的分形邊界。對於數學來說，當膨脹理論作為CMB的一個良好的解釋時，所有對Mixmaster宇宙的興趣都消失了。但我認為，Mixmaster宇宙還是值得研究的。

主要原因是我們認為廣義相對論中隱藏著更多的混沌，但相對論方程（有十個）是如此複雜，以至於我們不得不做出簡化。Mixmaster是尋找這些混沌區域的指南。

另一個原因是，Mixmaster宇宙可能會出現在量子尺度上，那裡的波動可以產生各種極端的幾何形狀。在這種情況下，在這種情況下，Mixmaster可能代表在普朗克長度的量子泡沫中的混沌氣泡。這可能有助於理解引力和真空漲落之間的關係，也有助於解釋暗能量。

Mixmaster 很重要的另一個原因是，混沌可能對解釋引力的熱力學至關重要，包括黑洞熱力學，以及廣義相對論中的隨機性。引力本身的隨機性是解釋時間的一個候選者，因為它在宇宙中產生了一個流動的方向，這種流動可能就是我們體驗時間移動的方式。

有一件事是肯定的，Mixmaster將永遠是一個明確的指標，即混沌生活在宇宙的跳動的心臟中。