在解決最小磁場問題或者其他類似問題時,引數方程特別是圓的方程是我們經常用到的一種處理問題的數學工作。本期我們著重來看一下。
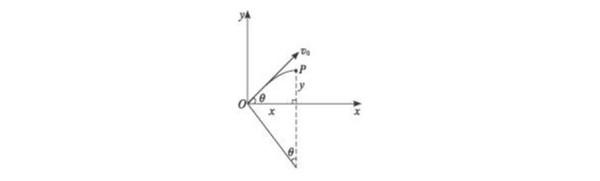
在xOy平面內有許多電子(質量為m、電荷量為e),從座標原點O不斷地以相同的速率v0沿不同方向射入第一象限,如圖所示。
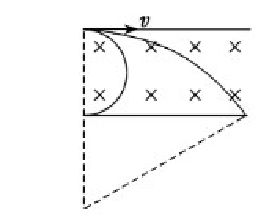
現加一個垂直於xOy平面向裡,磁感應強度為B的勻強磁場,要使這些電子穿過磁場區域後都能平行於x軸向x軸正向運動。求符合該條件磁場的最小面積。
解析:本題我們在前面也探討過,直接用結論是可以做的。今天我們再來重新審視一下本題。由題意可知,電子是以一定速度從原點O沿任意方向射入第一象限時,速度大小相同、方向不同,在磁場中做圓周運動的半徑r一定,即r=mv0/qB0。我們不用結論,而直接按照題意看是否可以解決。
如圖所示,
設任一電子速度v 0 與x軸夾角為θ,經磁場偏轉到速度方向變為平行x軸向右時的位置為P,P點座標為(x,y),則有:
x=r·sinθ ,y=r-rcosθ ,消去θ可得:x 2²+(y-r) ²=r ²
由上式可以看出P點位置在一個圓心為(0,r)、半徑為r的圓上的一段弧,此段圓弧應作為磁場的一個邊界。
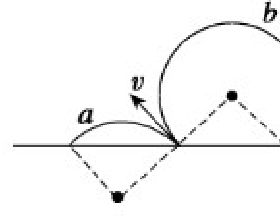
又沿+y方向射入的電子的偏轉軌跡是在以r為半徑、以(r,0)為圓心的圓上。兩個圓相交就可以得到最小磁場。可見軌跡圓的方程是引數方程應用的最為常見的應用。它有時候比我們背誦的結論更有通用性。
如果你有今日頭條app,麻煩順手點一下關注@中學物理知識傳播者,每天都會傾情奉獻一段小乾貨,我會繼續努力的!