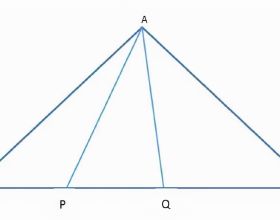
平面上透過一點的直線，要保證任意兩條直線所成的夾角相等，則直線最多可有幾條呢？

答案是3條直線。它們是正六邊形的透過對稱中心的那3條對角線。(或許有人說，有兩條線所成角是120°吧，它的補角啦)

等角線問題是空間中透過一個點的直線，使任意兩條直線的夾角都相等，則直線的數目最多為多少。

思考題：三維空間中的等角線最多有幾條？

數學助理教授趙宇飛(18年拿過MIT未來科學獎，國內正規媒體報道就是這個名字，我也就不用拼音了)說："在高維度上，事情開始變得有趣，而且可能的答案似乎是無限。”

但根據趙和麻省理工學院的數學家團隊，它們並不是無限的。他們解決了關於高維空間中等角線數量的幾何問題。這是已經困惑了數學界至少70年的難題。

他們的突破決定了可以放置的線條的最大可能數量，以便這些線條以相同的給定角度成對分開。趙與麻省理工學院的一組研究人員共同撰寫了論文。他們的論文將發表在2022年1月的《數學年鑑》上(ANNALS OF MATHEMATICS數學頂刊)。

他們藉助圖論的工具，使用譜圖理論發展出了全新的思想，為研究網路結構提供了新的數學工具。譜圖理論孕育了計算機科學中的重要演算法，如谷歌用於其搜尋引擎的PageRank演算法。

他們的純數學研究或對編碼和通訊領域有潛在影響。等角線是 "球形編碼" 的例子，後者是資訊理論中的重要工具，允許不同地址在一個嘈雜的通訊渠道上相互發送資訊。

最新結果建立在1973年P.W.H. Lemmens和J.J. Seidel一篇論文中提出的定理之上。

普林斯頓大學數學教授Noga Alon說："這是一個美麗的結果，為極值幾何學中精心研究的問題提供了一個令人驚訝的犀利答案，這個問題從60年代開始就受到了相當多的關注。”

"當時有一些好的想法，但後來人們被卡住了近三十年。"趙說。

這項研究得到了Alfred P. Sloan基金會和國家科學基金會的部分支援。另兩位合作者，姚和張透過數學系的本科生研究暑期專案(SPUR)參與了這項研究，而Tidor是他們的研究生導師。他們的成果為他們贏得了數學系的Hartley Rogers Jr. 最佳SPUR論文獎。

"這是SPUR專案最成功的成果之一，"趙說，"不是每天都能有一個長期的開放性問題得到解決。"

這項工作同時為譜圖理論提供了一個新的定理——一個有界的度數圖必須有亞線性的第二特徵值多重性。

"這個證明乾淨而漂亮。我們在一起研究這個問題時倍感快樂。"

https://phys.org/news/2021-10-mathematicians-geometry-problem-equiangular-lines.html