2000年5月24日,新罕布什爾州的克萊數學研究所列出了數學和計算機科學中七個未解決的問題。解決其中任何一個問題的獎勵是該研究所提供的一張100萬美元的支票。然而,直到今天,這些問題中只有一個被解決了,那就是龐加萊猜想(Poincaré Conjecture)——被俄羅斯數學家格里戈裡-佩雷爾曼解決。重要的是要認識到,這些問題的 "解 "是以數學證明的形式出現的,要麼否認,要麼確認該定理。其他六個未解決的問題之一是著名的P vs NP問題。
時間複雜度
對時間複雜度的研究可以得到很好的複雜度(下面解釋)。麻省理工學院的邁克爾·西普塞(Michael Sipser)教授因其在計算複雜性理論領域的傑出工作而聞名,他給出的標準定義是:
讓M是一個確定性的圖靈機( Turing machine),它對所有的輸入上都會停機(halt,停機問題是邏輯學的焦點,也是第三次數學危機的解決方案)。M的執行時間或時間複雜度是函式f:N→N,其中f(n)是M對任何長度為n的輸入所使用的最大步驟數。習慣上我們用n來表示輸入的長度。
看完定義應該比較懵逼吧?這到底是什麼意思呢?現在,讓我們降低維度來看這個問題。一個演算法的時間複雜度可以被描述為該演算法在計算機上對給定輸入長度的執行時間。確定一個給定程式的時間複雜度可能很困難,所以計算機科學家們開發了一種稱為漸近分析(asymptotic analysis)的估計表示式,也稱為大O表示。做好準備,另一個複雜的定義正在向你走來:
讓f和g是函式f , g : N → R+。如果存在正整數c和n0,使每個整數n≥n0,f(n)≤cg(n),則稱f(n)=O(g(n))。
當f(n)=O(g(n))時,我們說g(n)是f(n)的上限,或者更準確地說,g(n)是f(n)的漸近上限,以強調我們在抑制常數因素。
讓我們暫時跳過第一部分,更仔細地看一下定義的第二部分。我們將在這裡使用一個例子:
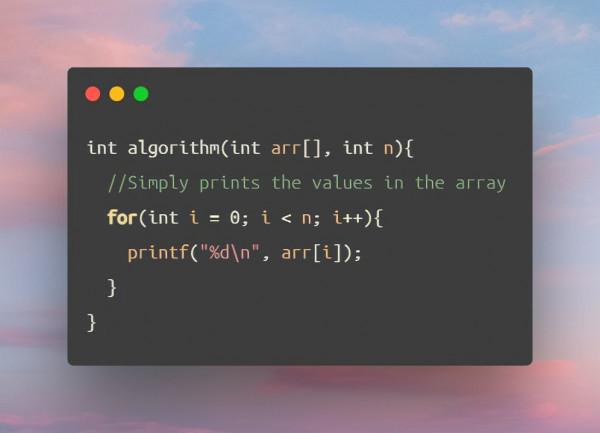
- 一個簡單的C語言for迴圈
為了找到這個演算法的漸進上限,我們必須首先分析各部分。如果本例中陣列n的大小為10,則迴圈將執行10次。在這種情況下,函式的上限將永遠是n的大小。因此,n是漸進的上限,計算機科學家用來描述這一事實的符號是O(n),這被稱為線性時間( linear time)。
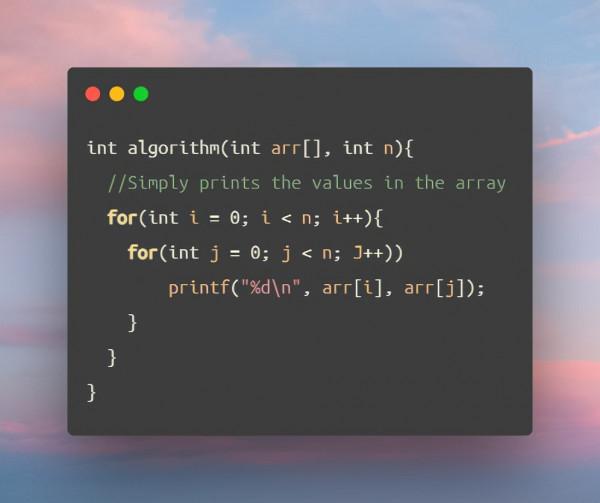
- 兩個for迴圈的 大O是O(n^2)
這裡的函式有兩個for迴圈,意味著如果n=10,它將被執行100次,或n*n次。大O的表達是O(n^2),或者說是平方時間(quadratic time)。
假設一個演算法,我們能夠確定其時間複雜度為f(n)=4n²+2n+12,這是否意味著大O將是O(4n²+2n+12)?重要的是再看一下定義的最後一部分,我們正在尋找漸近線,因此我們只需要增速最快的項(在這種情況下是4n^2),並且我們去掉常數(因為常數可以根據硬體差異和限制而改變),最終得到一個O(n²)的大O。
那麼這與上面簡單的兩個for迴圈具有相同的大O?是的!大O幫助計算機科學家視覺化演算法執行時間的上限,所以就所有目的而言,這兩種不同的演算法具有相同的大O。
下面是一些不同的大O複雜度的相互比較:
P類和NP類
現在我們對時間複雜度有了一定的瞭解,我們終於可以看看研究判定問題( decision problems)的P和NP了。判定問題是一個有答案 "真 "或 "假 "的問題。
P:P代表多項式,是兩者中比較簡單的。P類可以被描述為可由演算法在多項式時間內解決的問題的集合。
- O(n), O(n^2), O(n^3) 都是多項式時間的例子。
- 屬於P類的問題的例子包括乘法,或者尋找一個數組中最大的整數。
NP:NP代表非確定性多項式,這是兩類中比較複雜的,它有兩種不同的可能定義。更簡單的定義是。
在計算複雜性理論中,NP(非確定性多項式時間)是一個用於對決策問題進行分類的複雜性類。NP是一組決策問題,對於這些問題,答案是“是”,它的證明可以在多項式時間內被確定性圖靈機證明。
NP(Nondeterministic Polynomially,非確定性多項式)類問題是指一個複雜問題不能確定是否在多項式時間內找到答案,但是可以在多項式時間內驗證答案是否正確。
最好是看一個經典遊戲來幫助直觀地瞭解NP問題。
例子:數獨
數獨是我用來描述NP中問題類別的最常用的例子。
- 一個正在被演算法解決的數獨謎題
數獨是很容易解決的,所以上面的演算法並沒有花費多少時間來解決它。然而,如果這個數獨謎題從9x9增長到100x100呢?如果我們把數獨問題從9x9的輸入,概括為採取NxN,那麼這個問題很快就會變成一個NP問題。
數獨問題是很容易驗證的。這意味著,給定一個數獨問題的解,存在一個多項式時間的演算法,可以正確驗證該解是否正確。
- 一個已解決的數獨謎題
再次使用這個9x9的例子,你自己可以很容易地驗證這是否是一個正確的解,並且設計一個演算法來完成你自己的大腦在這種情況下所能完成的工作也是很簡單的。然而,要解決任何大小的數獨謎題的演算法似乎就不那麼簡單了,這也是事實。
更深入的研究:NP的完備性(完全性)
與NP相關的問題是NP的完備性問題。這些問題因其難度而聞名,因為它們沒有已知的多項式演算法解(O(n), O(n^2)...)。這些問題可以被認為是計算機科學中最棘手的問題。
- 在O(n)中執行100個元素要1秒的演算法,在O(n³)中執行要3個小時。這似乎是一個很大的跳躍,一個以O(2^N)執行的問題,100個元素需要300quintillion(百萬的3次方)年。因此,尋找一個多項式解比一個指數解更有價值。
確定一個問題是否是NP-完備性的過程如下。
- 確定問題是否在NP中(可在多項式時間內驗證或可由非確定性圖靈機解決)。
- 確定該問題是否是NP-Hard。
NP-Hard:當事情從複雜變成更復雜。
NP-Hard問題的定義如下:
非正式地講,NP-Hard問題與任何NP問題一樣難或更難。更確切地說,任何NP-完備性問題都可以在多項式時間內簡化為NP-Hard問題。
解決一個NP-Hard問題的演算法可以解決所有的NP-Hard問題,因為每個NP-Hard問題都可以被轉化成其他問題。這意味著解決一個NP-完備問題的方案也能解決所有其他NP-完備問題。
同樣值得注意的是,一個NP-Hard問題不一定在NP中(記住),如果它既是NP-Hard又在NP中,我們會把它歸類為NP完備,而且不一定是判定問題。
例子:路徑與總和
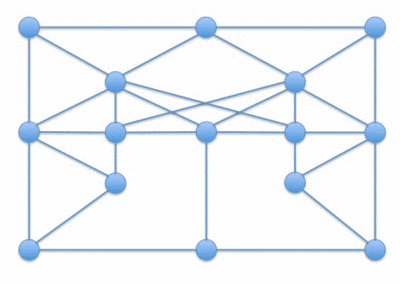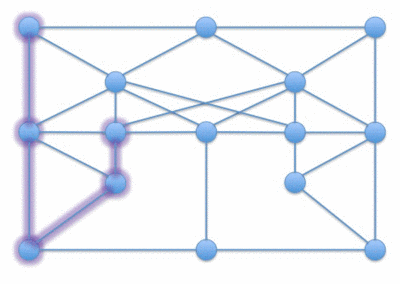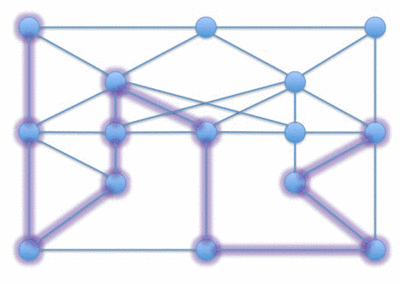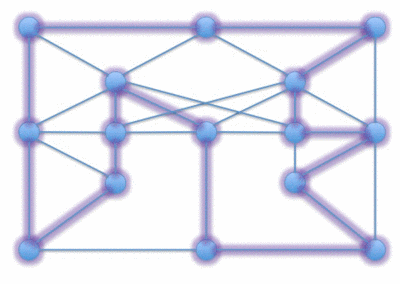
哈密頓路徑問題(Hamiltonian Path problem)問的是對於一個給定的圖,是否有一條路徑只訪問每個頂點一次。
- 哈密頓路徑
哈密爾頓路徑問題是一個NP完備性問題的例子。要驗證這個問題是否在NP中很簡單。
- 檢查每個頂點。
- 如果沒有通往某個頂點的路徑,則返回false。否則返回true。
子集和(Subset Sum problem)問題是,給定一個包含整數的集合S和一個目標和(target-sum)N,確定S中是否有一個子集的總和為N。
- S={1,3,5,6},N=4。答案是 "真",因為子集{1,3}的總和為4。
這個問題也是NP完備的。要驗證這個問題是否屬於NP,比上一個問題還要簡單:
- 將子集中的數字相加。
- 如果它們等於N,則返回true。否則返回false。
也許你很難相信,但是子集和問題和哈密頓路徑問題在函式上是等價的,因為它們都是NP-完備的。這意味著子集之和的解決方案可以轉化為解決哈密爾頓路徑問題。有大量的NP-完備問題,這只是其中兩個例子。
最後:P=NP?
P是否等同於NP?
大多數數學家和計算機科學家會說,No。但我們還沒有一個明確的證明。
- 普遍的共識是左邊的說法是正確的
重要的是要考慮到,P=NP只告訴我們存在多項式時間的解,而不是這些演算法是什麼。
然而,如果這些演算法確實存在,而且問題被解決了,那麼它不僅對計算機科學領域,而且對其他主要領域都會產生一些深遠的影響:
- 公鑰加密,或者說我們幾乎所有的個人和可識別資料是如何被儲存和保護的。
- 加密雜湊,或者說很多資訊是如何被加密的,以及像比特幣這樣的系統是如何被保護的。
- 計算基因組學,這個領域的一系列問題。
其影響可能是巨大的,因為到最後,我們實際發現最可用的演算法希望是O(n)或O(nlogn)和O(logn)--即使P=NP,如果演算法是O(n^100),它也沒什麼實際意義。
這是一個我們仍在努力解決的問題,也是一個也許永遠不會被解決的問題。
總結
- P類問題:所有可以在多項式時間內求解的判定問題構成P類問題。
- NP類問題:所有的非確定性多項式時間可解的判定問題構成NP類問題。
- NP-hard,指所有NP問題都能在多項式時間複雜度內歸遇到的問題。
- NP完備問題(簡單的寫法是 NP=P?):NP中的某些問題的複雜性與整個類的複雜性相關聯。這些問題中任何一個如果存在多項式時間的演算法,那麼所有NP問題都是多項式時間可解的。這些問題被稱為NP-完備問題(NPC問題)。