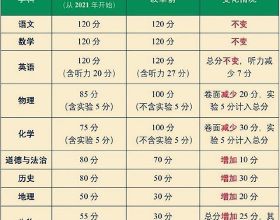
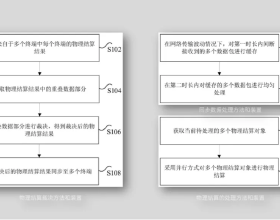
1 雙縫干涉概念
單色光照射到具有兩條狹縫的擋板上,這狹縫相距很近,通常在微米量級。從兩條狹縫發射出來的光波相位差恆定,頻率相同。兩束光在檔板後的空間相互疊加而發生干涉現象,在屏上產生了明暗相間的干涉條紋。當屏上的某點與兩縫的光程差是半波長的偶數倍時,形成亮條紋,是半個波長的奇數倍時,出現暗條紋。
2 定態的干涉光波
實驗室通常採用波長約為589nm的鈉黃光作為干涉光源,上圖中的a點就是光源所在處。鈉光燈可以看做是點光源,其發射的光波為球面波。球面波在一個平面上的傳播方程可以簡單寫為:A=A0 * cos(w(t-r/v)+q) ,其中A為振幅,w為角頻率,r為某點離光源的距離,t為傳播時間,q為初始相位。為了方便計算空間各點的振幅,該公式可以用python定義為一個函式方便重複呼叫:
def func_A(t,q,x,y,x0,y0):
r = ((x - x0) ** 2 + (y - y0) ** 2) ** 0.5
A=np.cos(w*(t-r/v)+q)
return A
當光波到達b,c兩條狹縫時,根據惠更斯原理,b,c兩點會成為新的“子波源”,因此,b,c兩個波源發射的光波具有相同的頻率,恆定的相位差,成為相干光。假設兩波源的初始相位都為零,根據上述python語言的函式定義,b,c兩點的光波傳播函式分別為:
b_A = func_A(t,0,x, y, 0, 2)
c_A = func_A(t,0, x, y, 0, -2)根據光強的計算公式,可以得到光強是正比于振幅A的平方。干涉場空間各點的振幅為兩振幅的疊加,也就是b_A+c_A,所以空間的各點光強定義為函式:
def f(t,x, y):
A1 = func_A(t, 0,x, y, 0, 2)
A2 = func_A(t,0, x, y, 0, -2)
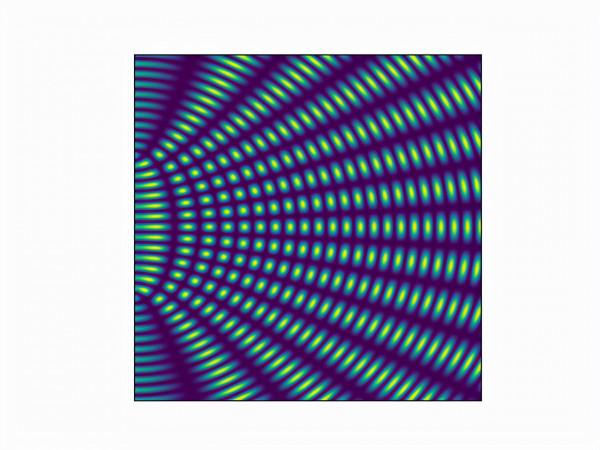
return ((A1+A2)**2)在某時刻干涉光場的解為f(0,x, y),採用matplotlib繪相簿將干涉場各點的光強顯示出來。執行ax.imshow(f(0,x, y)),就可以看到等間距的明暗光波疊加的效果。
3 動態的光波效果
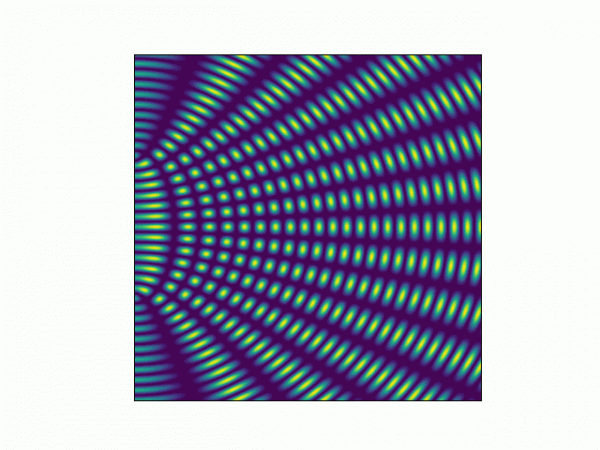
計算多個時刻的定態光波干涉場,然後將這些影象製作為影片或動畫就可以看到動態光波的效果,下圖就是干涉光波傳播的效果動畫。
4 在現實中人眼看見的效果
我們上面介紹了光波的定態和動態效果圖,但並不代表人眼所看到的就是明暗相間的散點。我們人眼所看到的效果是長時間光照射的疊加效果,比如,我們在看電風扇轉動時,你只能看見一個圓盤,而不會看到三個葉片。再比如,顯示屏是逐行掃描的,而我們看到的卻是一幅影象。這一切都是由於視覺暫留效應,我們人眼並不能分辨出很短時間內的影象變化。干涉場也是這樣,光波都是在飛秒時間內變化,我們無法分辨短時間光明暗的變化。在干涉場內,如果一個地方時亮時暗,我們看起來就是亮;如果一個地方一直暗看起來才會是暗。用Python模擬這種效果,就是簡單將各個時刻的光波場疊加,就可以看到明暗相間的條紋。
z=f(0,x, y)
for i in range(1,10):
z=f(i*0.3,x, y)+z關於雙縫干涉的python模擬先介紹到這裡,最後附上原始碼:
import numpy as np
import matplotlib.pyplot as plt
import random
v=3*(10**8)*(10**6)*(10**(-15))
L=0.589
w=2*np.pi*v/L
def func_A(t,q,x,y,x0,y0):
r = ((x - x0) ** 2 + (y - y0) ** 2) ** 0.5
A=np.cos(w*(t-r/v)+q)
return A
fig, ax = plt.subplots()
ax.set_xticks([])
ax.set_yticks([])
def f(t,x, y):
A1 = func_A(t, 0,x, y, 0, 2)
A2 = func_A(t,0, x, y, 0, -2)
return ((A1+A2)**2)
x = np.linspace(0, 8, 1000)
y = np.linspace(-5, 5, 1000).reshape(-1, 1)
ax.imshow(f(0,x, y))
plt.show()