在古希臘天文學家喜帕恰斯巧妙利用三角測量法粗略計算出地月距離之後大約1900年,法國天文學家拉卡伊(1713-1762)和他的學生拉朗德(1732-1807)利用三角測量法首次精確計算出地月距離。
1752年,20歲的拉朗德來到柏林(地理位置:東經13.40°,北緯52.52°),當時,他的老師拉卡伊正在非洲南端的好望角(地理位置:東經18.47°,南緯34.36°)。這兩個地方經度相差5°,緯度相差86.88°。他們同時在這兩個地方進行觀測,首次用三角法來精確測定月亮的距離。
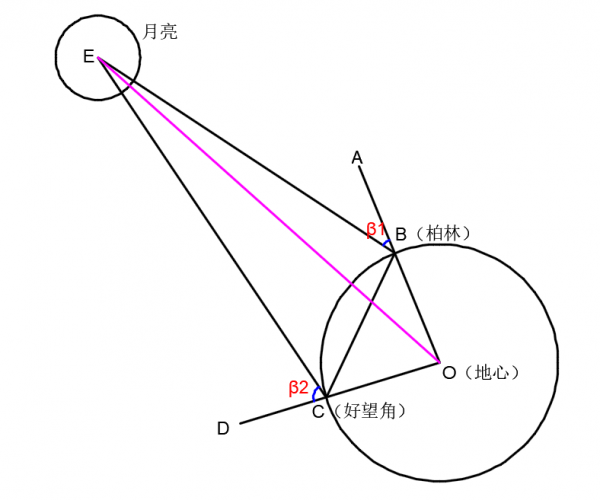
如下圖1所示,當夜幕降臨時,月亮從地平線上越升越高,當它到達最高點,即圖中的E點。這時拉朗得在B點(柏林)測出月亮的天頂距β1(即離開頭頂方向的角度),它用角ABE表示,拉卡伊在C點(好望角)測出月亮的天頂距β2(即離開頭頂方向的角度),它用角DCE表示。圓弧BC所對應的圓心角BOC,正好等於B、C兩地之間的緯度差,即柏林與好望角之間的緯度差。因為OC=OB=地球半徑,角COB已知,所以BCO=角CBO=(180-角COB)/2,BC的長度也可以求出來。又角DCE、角ABE、角BCO、角CBO的大小都已知了,於是角ECB與角EBC的長度也能很容易求出來。這時三角形ECB的底邊BC與兩個底角ECB、EBC都是已知的,月地距離EC與EB就能很容易求出來了。
如果要計算出地球圓心到月球圓心的距離,也即圖1中EO的長度,可以用下面的方法進行求解。
如圖2所示,O、E分別是地球和月球球心,從E點引出一條切線(該切線與柏林、好望角處於同一經度上)與地球相切於P,設地球半徑為r,角OEP=θ,地月球心距離為d。
則地月距離:d=OE=r/sinθ……①
如圖3所示,MN是地球赤道面上的直徑,B點(柏林)的緯度為α1(角MOA=α1)、月亮的天頂距為β1(角ABE=β1),C點(好望角)的緯度為α2(角MOD=α2)、月亮的天頂距為β2(角DCE=β2)。設角BEO=θ1,角CEO=θ2,地球半徑為r,地月球心距離為d。
在三角形EOB中,根據正弦定理,則有:
r/sinθ1=d/sin(Π-β1)=d/sinβ1……②
由式子①②可得:sinθ1=sinβ1*sinθ……③
將θ1=β1-角EOB=β1-(α1-角EOM)=β1-α1+角EOM代入式子③中,可得:
sin(β1-α1+角EOM)=sinβ1*sinθ……④
在三角形EOC中,根據正弦定理,則有:
r/sinθ2=d/sin(Π-β2)=d/sinβ2……⑤
由式子①⑤可得:sinθ2=sinβ2*sinθ……⑥
將θ2=β2-角EOM=β2-(α2+角EOM)=β2-α2-角EOM代入式子⑥中,可得:
sin(β2-α2-角EOM)=sinβ2*sinθ……⑦
考慮到θ1(β1-α1+角EOM)、θ2(β2-α2-角EOM)兩角很小,這兩個角的正弦值近似等於這兩角的值,於是式子④與式子⑦變為:
β1-α1+角EOM=sinβ1*sinθ
β2-α2-角EOM=sinβ2*sinθ
兩式相加可得:sinθ=(β1+β2-α1-α2)/(sinβ1+sinβ2)
拉朗德與拉卡伊求得的結果是 = 57′,與 近代測得的數值57′2.6″ 相當接近,從而求得:
d=r/sinθ=r/sin57″≈60.3r。
好了,這一講就到這裡了。
我是科學發現之歷程,一個致力於科普數學、物理的科技媒體。想了解更多相關的知識,關注微信公眾號科學發現之歷程,期待你的到來~