斯里尼瓦瑟·拉馬努詹( Iyengar Ramanujan)是印度自學成才的天才。他愛數字勝過一切,他幾乎每天甚至每小時都會發現一個新的定理。但根據他自己的說法,這些定理是他夢中的女神Namagiri告訴他的。不管怎樣,他的天才永遠不會受到質疑。拉瑪努詹,在他在世的最後一年發現了2000個新的定理,現在這些定理被儲存在劍橋大學圖書館的三卷本中,被稱為 "拉馬努詹遺失的筆記本",在他30歲的時候就去世了。
雖然拉馬努詹的大部分研究都超出了大多數人的智力範圍,但有一項研究非常著名,幾乎所有對數學感興趣的人都知道,那就是他證明了“所有自然數之和是負數”這一荒謬的結論。
-1/12也恰好出現在弦理論中(不是霍金的那個,而是玻色弦理論),而這個理論恰好在相當大的程度上解釋了我們的宇宙!但這是真的嗎?這絕對是說不通的,對吧?那看看拉瑪努詹本人為這個看似不現實的等式提出的實際證明。
拉馬努詹從兩個數列開始:
- T=1-2+3-4+5-6+7-...
- S=1-1+1-1-...
首先考慮第二個式子:
- S = 1-1+1-1+1-...
接下來,他作了一點變換:
- S = 1-(1-1+1-1+1-...)
如果你仔細看,括號內的“東西”是零,對吧?
這裡,我要提醒的是,當涉及無窮時,不要相信你的直覺,這是我在另一篇文章中詳細討論過的。
調和級數——自然真理是如何隱藏在數字中的,永遠不要相信直覺
我們繼續……根據我們的直覺,括號內的“東西”等於零,那麼就有:
- S = 1-S
- 2S = 1
- S = 1/2 - - - - [1]
重新排列後,我們得到的結果是,這個級數等於1/2。
接著是第一個等式。
- T = 1-2+3-4+5-6+7-...
現在我們把兩個T相加。
- 2T = (1-2+3-4+5-6+7-...) + (1-2+3-4+5-6+7-...)
這裡,我們把1從其中一個括號裡拿出來(這只是拉馬努詹眾多技巧中的一個),你會習慣的。
- 2T = 1 + (-2+3-4+5-6+7-...) + (1-2+3-4+5-6+7-...)
重新排列,我們得到:
- 2T = 1 + [ (-2+1)+(3-2)+(-4+3)+...]
看到了嗎?
- 2T = 1 + [-1+1-1+1-...]
- 2T = 1-1+1-1+1-...
- 2T = S = 1/2
- T = 1/4
沒有什麼問題,對吧?
現在,取所有整數之和為U=1+2+3+4+...,我們用U減去T:
- U-T = [1+2+3+...]-[1-2+3-4+...] 。
- U-T = [(1-1) + (2-(-2)) + (3-3) + (4-(-4))+...
加起來,得到:
- U-T=4+8+12+...。
再次重排,得到:
- U-T=4(1+2+3+...)=4U
- U-4U = T
- 3U = T
因為我們已經知道T=1/4:
- 3U = -1/4
- U = -1/12
因此,1+2+3+...=-1/12,但實際上是這樣嗎?我之前提醒過,涉及到無窮時,不要相信你的直覺!
答案是否定的! 為什麼這個答案是錯誤的,原因來自於實分析中最基本的概念之一,收斂。如果你還沒有注意到,我們談到的第一個等式S,只不過是格蘭迪級數( Grandi’s Series)。
- S = 1-1+1-1+1-...
S可以有兩個可能的值,當我們考慮偶數項之和時為0,當我們考慮奇數項之和時為1,但S作為一個整體沒有任何特定的解,因為它既不考慮偶數項之和,也不考慮奇數項之和,而是無限的級數。你可能會問,為什麼格蘭迪級數沒有解(答案),而其他許多無限級數卻有解,這個問題的答案將引導我們瞭解為什麼拉馬努詹的無限級數是錯誤的。
讓我們把S寫成求和的形式,讓它看起來更 "數學 ":
- 其中n是一個整數,當n趨向於無窮時,S變成了格蘭迪級數
我們觀察到,當n從1到∞變化時從S得到的值,這些值會在0和1之間來回“跳轉”,或者換句話說,S的值不“收斂”於任何東西。
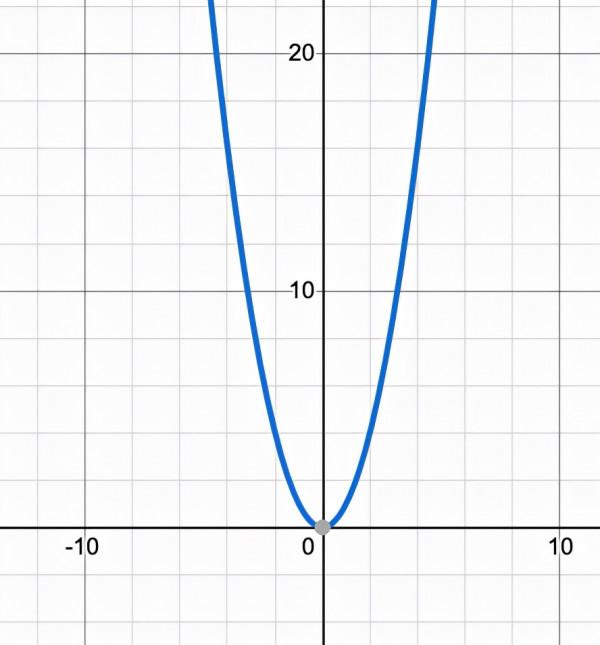
為了弄清收斂的概念,讓我們考慮一個更簡單的函式。
從圖中可以看出,隨著x值的增加,函式f(x)慢慢地趨向於1,圖形變得平坦。或者我們可以說,該函式收斂於1。
而在另一方面,像這樣的函式:
是不收斂的,因為當x的值增大時,函式g(x)趨向於∞,不像f(x)那樣收斂到常數1。
拉馬努詹無限級數錯誤的關鍵原因是認為S等於1/2,這在實際情況下是不可能的,儘管它被證明等於1/2,因為S是不收斂的,也就是說,即使我們取S的無限項之和,我們要麼得到0,要麼得到1,再加項會導致同樣的結果,0或1。這裡的S是一個交替的級數,即對於奇數項之和,得到一個特定的結果1,而對於偶數項之和,得到另一個結果0,而且數值一直在變化。
對於第二個級數T,也可以發現類似的錯誤。
- T = 1-2+3-4+5-6+7-...
重新排列和簡化後我們得到:
- T = (1-2)+(3-4)+(5-6)+...
- T = -1-1-1-...
或者用更多的數學術語來說。
它與最初發現的1/4的值不一致是有道理的,因為我們曾用S=1/2來找到相同的值,而我們已經看到,S=1/2是絕對錯誤的。
此外,作為所有自然數之和的U可以寫成。
- U以極限的形式寫出來
從U的極限表達中可以看出,n(n+1)/2不能被簡化以得到∞以外的結果。因此,由於所有自然數之和n(n+1)/2絕不是收斂的,我們不能期望它收斂到-1/12。
注意到前面討論的弦理論中出現的-1/12是很有趣的,這將是下一篇文章的主題了。