走進高維空間之“維度魔咒”，所有的“鄰居”都去哪了？

歡迎來到 "走進高維空間系列 "的第五部分，在這裡我們將探索高維空間的一些奇怪和反直覺的奇觀。距離高維空間系列第四部分：”走進高維空間——機率論與高維空間的深層次聯絡“已經有一年多了。在閱讀第五部分之前，我建議先瀏覽以下前四部分內容。

簡單回顧以下前四部分的內容：

第一部分我們得出：在無限維空間中球體的體積都集中在邊界上，我們只能知道這個結論，但是無法想象！
第二部分的結論是，在高維空間中，內切於球內的立方體不完全在球體以內。
.在第三部分中，我們推匯出，在無限維空間中，點與點之間的距離都是相等的。
第四部分討論的是高維空間與機率論的聯絡。

這些瘋狂的、無法想象的高維空間現象讓人興奮，我們只能藉助數學等工具去理解它們的真正含義。這篇文章，我們將見證這些奇蹟之一是如何影響一個廣泛使用的統計工具的。讓我們開始吧！

預測問題

在各種領域中，人們通常會根據一個或多個預測變數的值來預測某個響應變數的值。也許我們希望預測一個病人在出院後30天內再次入院的機率（響應），因為有各種人口統計學和臨床特徵（預測因素例如，年齡、是否有併發症、實驗室測量）。或者，我們希望根據房屋的各種特徵（如鄰里關係、臥室數量、面積）來預測房屋的銷售價格。或者我們希望根據各種環境和農業特徵（如降雨量、土壤成分、害蟲管理策略）預測作物產量。

可靠地預測某些響應變數的值的能力是非常強大的，有大量的方法可以解決這類問題，每種方法都有不同的優點和侷限性。今天，我們將特別關注其中的一個方法，因為它非常直觀，最重要的是，它給我們提供了一個觀察高維空間的一些奇蹟的機會。

K-近鄰演算法（K-Nearest Neighbors）

如果我們想用一組特定的預測值來預測一個新的資料點的響應值，我們只需檢視訓練資料，找到所有具有完全相同的預測值的資料點，並計算出對這些訓練資料點觀察到的響應值的平均值或中位數。問題是，我們通常沒有如此豐富的訓練資料，而且很少有跨越所有可能的預測值組合的訓練資料。當我們想預測一個新的資料點的響應值時，我們可能有一些類似的訓練資料點的響應值，但沒有完全相同的預測值組合。那該怎麼辦呢？構建一個模型。

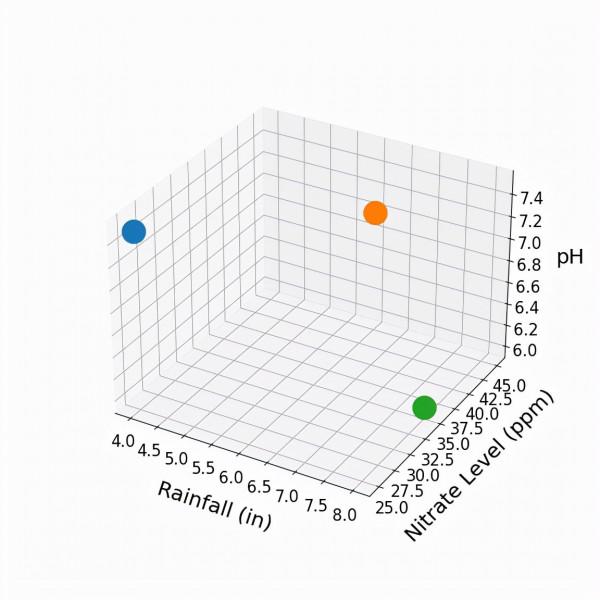
為預測-響應關係建模的一種方法被稱為K-近鄰演算法。為了理解這種方法，讓我們把預測變數看作是代表一些高維的預測空間。也許你想知道這意味著什麼，但這其實很簡單，如果我們正在處理番茄作物資料，也許在第一軸（即維度）上有總降雨量，第二軸上有土壤硝酸鹽水平，第三軸上有土壤pH值，第四軸上有平均溫度，等等。因此，我們的每一個數據點都代表了高維空間中的一個點，它在該空間中的座標取決於它對每個預測變數的值。例如，讓我們看一下三維作物預測空間中的幾個點。

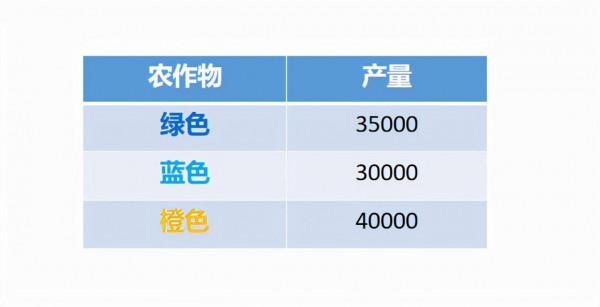
這裡，綠色的點代表降雨量為8、土壤硝酸鹽含量為35、pH值為6的作物；藍色的點代表降雨量為4、土壤硝酸鹽含量為25、pH值為7.5的作物；而橙色的點代表降雨量為6、土壤硝酸鹽含量為45、pH值為7的作物。假設我們知道與這些西紅柿作物中的每一種相關的作物產量。

通常情況下，我們會將產量（即響應變數）作為一個額外的軸/維度進行視覺化，但我在這裡沒有這樣做，因為我們只能將三個維度視覺化化。

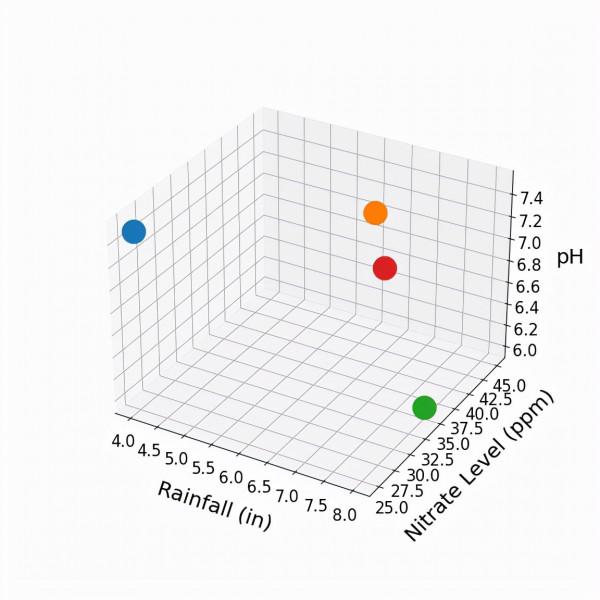
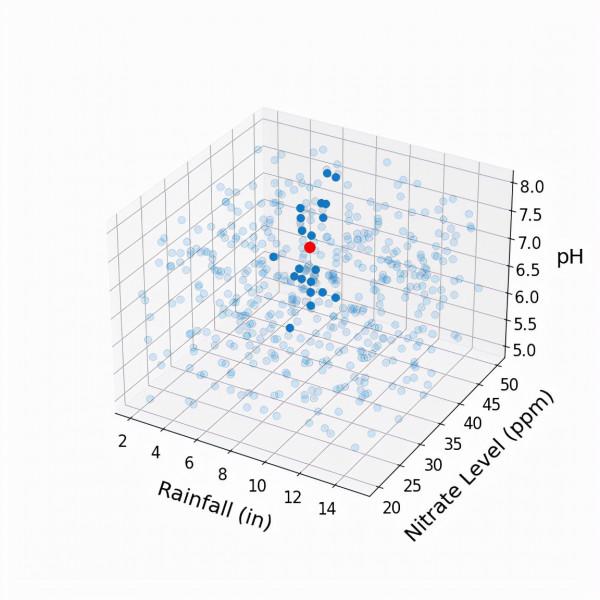
比方說，現在是春天，我們正在種植新的西紅柿作物。我們有土壤的硝酸鹽水平和pH值，而且我們對預期的降雨量有一個很好的概念。我們把這個新作物表示為下面的紅點。

利用原來三個點的作物特性和產量，我們如何估計新的紅色點的產量？有一種方法，叫做（單）近鄰法，就是用原來三個點中最接近的作物產量來估計。我們會期望最近的點有大致相似的降雨量和土壤成分。看起來橙色點離紅色點最近（產量為40000）。然而，從一個數據點推匯出估計，不覺得有點不靠譜嗎？也許與橙點相關的產量是一個意外，同樣的特性在其他年份產生的產量可能會低得多。只有3個數據點，沒有什麼操作空間，但如果有數百個資料點呢？

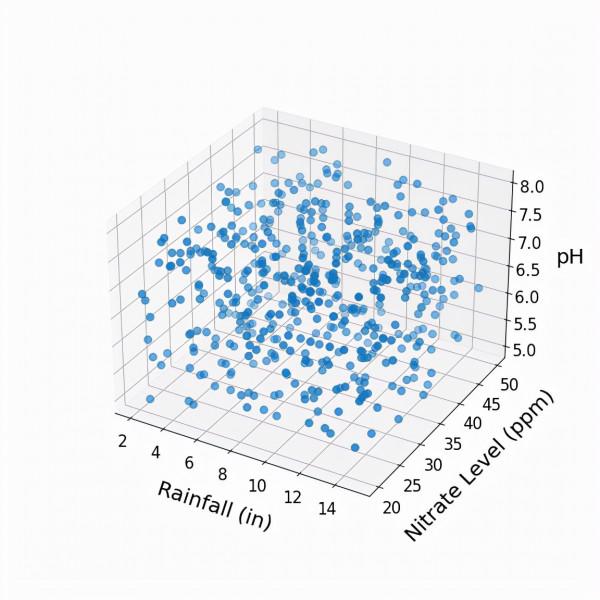
現在，加入紅點所代表的新作物。

同樣，我假設我們知道所有藍點的作物產量，並希望利用這些資訊來估計紅點的作物產量。我們是否應該再次採用K-近鄰演算法？下面，我們找出離紅點最近的20個“鄰居”。

為了估計紅點的作物產量，取這20個近鄰的作物產量的平均值似乎很合理，對嗎？在這個例子中，我們只是在三維空間中運算，但這個方法可以推廣到任何維度。

我們如何定義 "最近的"？普通的歐幾里得距離？還是像馬氏距離（ Mahalanobis distance ）這樣更細微的東西（它包含了不同預測因子之間的變化和關係）？這些問題都很重要（而且超級有趣），但答案與我們現在所要討論的無關，所以我將把它們放在以後的文章中。

讓我們繼續向前進：高維空間！

鄰居們，你們好！

在接下來的部分中，我們將從有趣的應用例項（例如病人、家庭、農作物）中“撤退”，進入一個簡化的空間。想象一下，我們正在處理只有一個預測變數和一個響應變數的資料；因此，預測空間只有一個維度。我們還可以想象，預測變數的值是沿著預測變數的範圍均勻分佈的。為了簡單起見，我們使用一個只能在-0.5和0.5之間取值的預測器，這樣，預測器的範圍是一個單位長度。

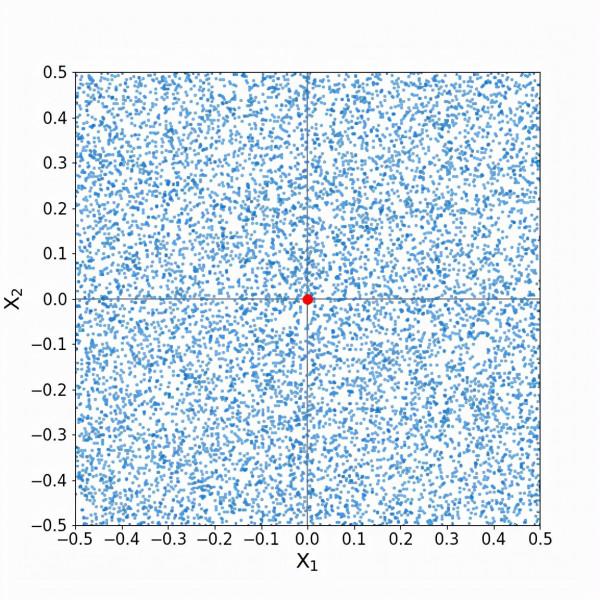
同樣，假設我們有一組資料點的預測值和響應值（稱為訓練資料點，因為這些是用來訓練K-近鄰模型的點）。讓我們用藍色來說明這些訓練資料點。

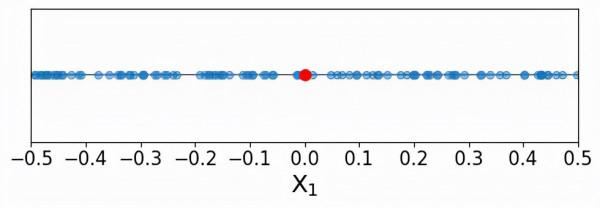
我們可以看到，訓練點似乎是沿著單一預測器的所有可能值均勻分佈的。現在，我們要預測一個新的點（稱為索引點）的響應值，下面用紅色表示。

正如我們上面所學到的，K-近鄰演算法的一般想法是確定在預測器空間中與索引點最接近的訓練資料點，然後利用這些訓練點的響應值來估計索引點的響應值。重要的是，我們只使用預測器空間中靠近的訓練點來為估值提供資訊。如果使用在預測空間中很遠的訓練資料點，那麼它們可能不能很好地代表索引點的響應值，而我們的最終估計值可能與事實相差甚遠。

在這個例子中，假設使用最接近索引點的10%的訓練資料點，從索引點出發，需要在預測器空間中達到多遠才能捕獲10%的訓練資料？更具體地說，需要在鄰域中包括多大比例的預測值範圍？

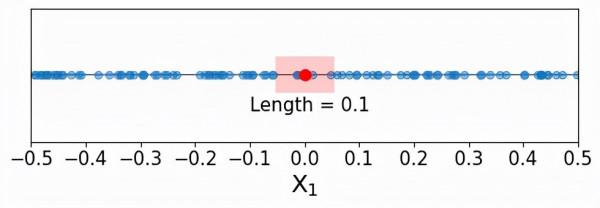
單預測器的情況實際上很簡單。因為訓練資料點是沿著單一維度均勻分佈的，而預測器的範圍是[-0.5,0.5]，為了捕獲10%的訓練資料點，只需要包含預測器範圍的10%。如下圖所示：

看上去很合理，對嗎？我們不需要離索引點太遠，就可以把10%的訓練資料納入，只需要在兩個方向上取0.05個單位。目前看起來沒什麼特別，也許還有點無聊。讓我們看看當入一個更高的維度時會發生什麼。

鄰居的秘密

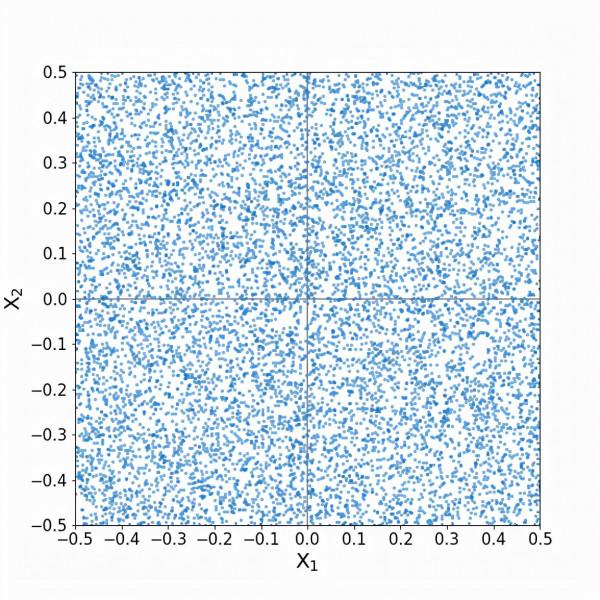
假設我們有兩個預測器，每個預測器的範圍是-0.5到0.5，訓練資料點沿兩個維度均勻分佈。

這是我們的索引點：

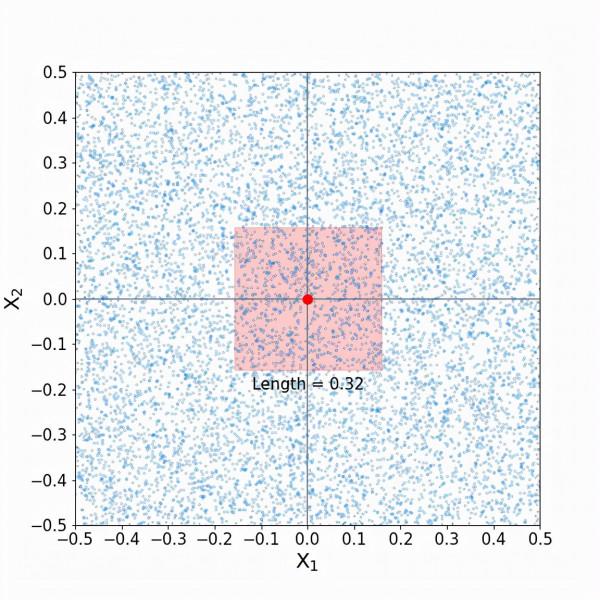
同樣，我們希望捕捉10%的訓練資料點。要做到這一點，每個預測器的範圍中必須包括多少比例的鄰居？也許我們可以把上面看到的擴充套件一個維度，我們將需要第一個預測器的10%和第二個預測器的10%。讓我們來看看（我把訓練點淡化了一些，以便更好地觀察）：

這是高維空間的奧秘中的另一個轉折點！在單維空間中，我們只需要在索引空間的任何一個方向上取0.05個單位就可以捕獲10%的訓練資料。而現在，我們似乎必須從索引點的任何一個方向取0.16個單位，才能捕獲10%的訓練資料！就其預測值而言，鄰域外圍的訓練點真的與索引點那麼相似嗎？答案最終將取決於資料的性質，但必須承認，當我們的目標是包括預測值與索引點儘可能相似的點時，包括每個預測器的近三分之一的範圍似乎有點寬泛了。

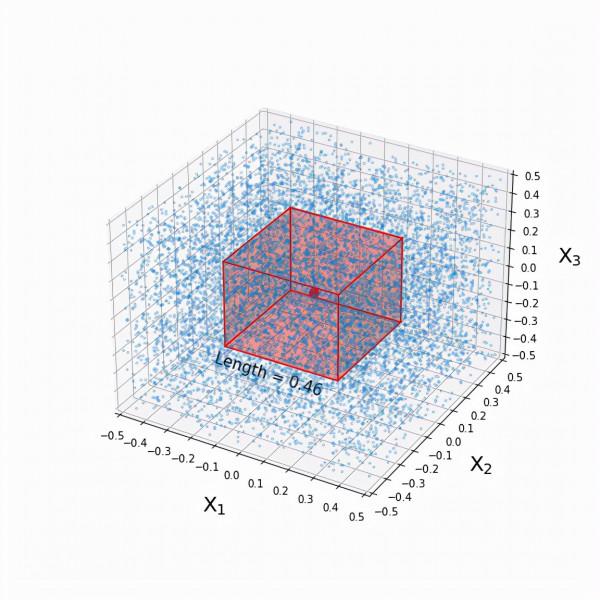
我們繼續，向三維預測器空間邁進! 下面是我們沿三個維度均勻分佈的訓練資料點雲（左），以及索引點（右）。

也許你已經知答案，但我再次提出問題：為了獲得10%的訓練點，應該怎樣取值？

將近50%! 讓我們消化一下：

在單維中，只需要包括單個預測器範圍的10%，就可以定義一個包括10%的均勻分佈的訓練資料的鄰居。
在兩個維度上，需要兩個預測器的範圍各佔32%。
在三個維度上，需要三個預測器範圍中的每一個的46%!

這裡的基礎數學其實很簡單，真正的精彩在最後。

讓我們用一個例子來說明這個問題吧，記得農作作物例子嗎？ pH值的範圍是0-14。如果我索引點的pH值為7，那麼就要在一個維度上包括pH值為6.25-7.75的訓練點（直覺上似乎是合理的，對嗎？），在兩個維度上包括4.6-9.4（這合理嗎？），在三個維度上包括3.55-10.45（這似乎開始離譜了）。將這些點稱為鄰居還有意義嗎？

延伸

在應用統計學中，使用幾十個、幾百個、甚至幾千個預測因子是很常見的。如果在三個維度中，每個預測器的範圍有近50%是用來捕捉10%的訓練資料的，那麼在10個維度中呢？100個維度呢？

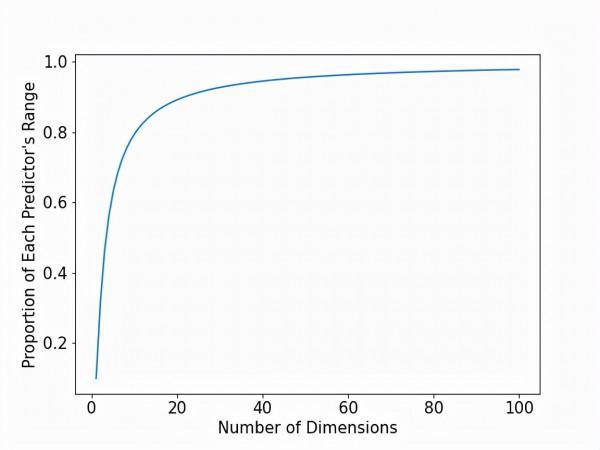
下面的圖對1到100個維度之間的每一個維度回答了這個問題。具體來說，我們把維度（即預測器）的數量放在X軸上，把每個預測器的範圍比例（捕獲10%的訓練資料所需）放在Y軸上。

在圖的最左邊，我們看到了在一維、二維和三維方面的情況。然而，當達到10個維度時，幾乎需要每個預測器的80%的範圍！在50個維度時，需要95%的預測器範圍。到了100個維度，需要98%！

我們的目標是確定那些預測值與索引點儘可能相似的訓練點。在這些更高的維度上，幾乎把預測器的任何值的點視為鄰居，並將使用它們來估計索引點的響應值。在我們設計的具有均勻分佈的預測因子的例子中，應用K-近鄰演算法在一個維度上似乎是完全合理的，但在更高的維度上很快就會變得離譜。真實的資料集不會和我們探索的資料集一模一樣，但這種需要進一步深入預測器空間來尋找附近點的想法依然存在。

所有的鄰居都去哪兒了？

讓我們來探討一個稍微不同的問題。之前，我們調查了在每個維度上取多少範圍才能捕獲10%的訓練資料。現在，讓我們看看，如果把鄰居的邊界限制在每個預測器範圍的10%，能找到多少個鄰居。在K-近鄰演算法的背景下，在空間上與索引點接近的訓練點似乎很適合為索引點的響應值的估計提供資訊。在一個維度上，一個包括10%的單一預測者範圍的鄰域包含了10%的訓練資料。在更高的維度上會發生什麼？讓我們來看看。

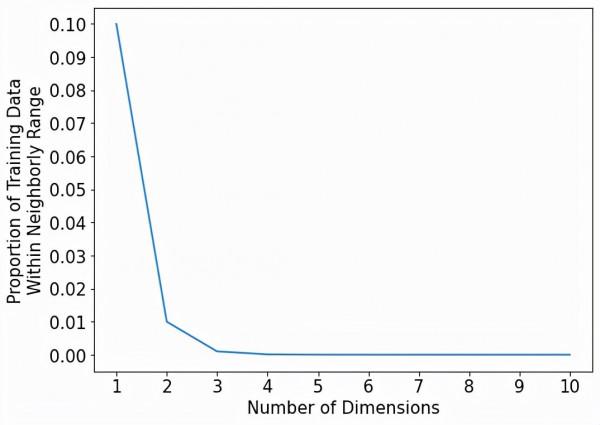
下面的圖在X軸上顯示了從1到10的維度，在Y軸上顯示了覆蓋每個預測器範圍的10%的鄰域所捕獲的訓練資料的比例。

所有的鄰居都去哪了？同樣，在一個維度上，鄰域覆蓋了10%的訓練資料。在二維，只有1%的訓練資料! 如果我們把一個索引點的鄰域定義為覆蓋每個預測者範圍的10%，那麼一個10維的鄰域將只包括訓練資料的0.00000001%。

讓我們用訓練資料點的實際數量來重新定義這些數字，而不是百分比和比例。比方說，有100,000個訓練資料點。這意味著，10維鄰域平均來說，甚至沒有捕捉到一個數據點（它將捕捉到0.0001個數據點）。這意味著，平均而言，每一萬個鄰域中，我們只能捕捉到一個鄰域！這意味著很多空的鄰域。這就是大量的空鄰居！

因此，用一個直觀合理的鄰域大小（覆蓋每個預測因子範圍的10%），在更高維度上基本上沒有鄰域。而這裡只到了10維！如果是100維，100萬維呢？

你已經進入了一個新的領域。進入了沒有鄰居的地方！鄰居們都去哪兒了？為什麼這些空間如此空曠？這些都是貫穿於高維空間的永恆的問題，這些問題引起了（並困擾著）許多統計學家，被精緻地稱為維度詛咒！