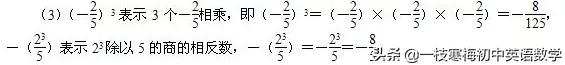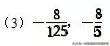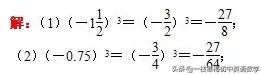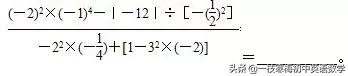第一次月考【有理數的乘除法】複習專練
例1. 計算:(1)5×(-4)
(2)(-4)×(-9)
(3)(-0.6)×(-5)
(4)3/7×(-7/9)
解:(1)5×(-4)=-(5×4)=20
(2)(-4)×(-9)=4×9=36
(3)(-0.6)×(-5)=0.6×5=3
(4)3/7×(-7/9)=-(3/7×7/9)=-1/3
指導:(1)(4)題是異號兩數相乘,先確定積的符號為“-”,再把絕對值相乘;(2)(3)題是同號兩數相乘,先確定積的符號為“+”,再把絕對值相乘。
例2. 計算:(1)(-4)×9×(-2.5)
(2)(1/4+1/3-1/6)×(-48)
解:(1)(-4)×9×(-2.5)
=(-4)×(-2.5)×9=10×9 =90
(2)(1/4+1/3-1/6)×(-48)
=1/4×(-48)+1/3×(-48)-1/6×(-48)
=(-12)+(-16)-(-8)
=-20
指導:(1)用乘法交換律和結合律,(2)用乘法分配律。在運用乘法對加法的分配律時,不要漏乘某個加數或弄錯符號,要細心。
例3. -3的倒數是( )
A. -1/3 B. 1/3 C. -3 D. 3
解:A
指導:倒數概念以及有理數除法運算是中考命題熱點。求一個數的倒數,用1除以這個數的商即是。注意:負數的倒數是負數,0沒有倒數。
例4. 計算(-16)÷5×1/5
解:(-16)÷5×1/5=(-16)×1/5×1/5=-16/25
指導:這是一道乘除混合的同級運算題,沒有括號, 按照自左到右的順序運算,不應先算5×1/5。
例5. 中百超市推出如下優惠方案:
(1)一次性購物不超過100元,不享受優惠;
(2)一次性購物超過100元,但不超過300元一律九折;
(3)一次性購物超過300元一律八折;某人兩次購物分別付款80元,252元,如果他將這兩次所購商品一次性購買,則應付款( )。
A. 288元
B. 332元
C. 288元或316元
D. 332元或363元
解:C
指導:本題滲透了分類討論思想。當252元的實際價值是在300元以內時的實際價值應為:
252÷0.9=280元,
故應付款(280+80)×0.8=288(元);
當252元的實際價值是在300元以上時的實際價值應為:252÷0.8=315(元),
故應付款(315+80)×0.8=316(元)
【思想方法小結】
乘除法運算中同學們要善於“轉化”,除法轉化為乘法,複雜的轉化為簡單的,異號轉化為同號。
【模擬試題】(答題時間:60分鐘,滿分100分)
一. 選擇題(每題4分,共20分)
1. 一件標價為250元的商品,若該商品按八折銷售,則該商品的實際售價是( )
A 180元 B 200元 C 240元 D 250元
2. 如果a/b>0,b/c>0,則下列說法錯誤的是( )
A. ac<0 B. ab>0
C. ac>0 D. bc>0
3. 下列說法錯誤的是( )
A. 小於-1的數的倒數大於其本身;
B. 大於1的數的倒數小於其本身
C. 一個數的倒數不可能等於它本身
D. (m-n)(其中m≠n)的倒數是1/(m-n)
4. 下列說法不正確的是( )
A. 一個數與它的倒數之積是1
B. 兩個數的積為1,這兩個數互為倒數
C. 一個數與它的相反數之商是1
D. 兩數之商為-1,這兩個數互為相反數。
﹡5. 已知abc<0,a>c,ac<0,則下列結論正確的是:( )
A. a<0,b<0,c>0
B. a>0,b>0,c<0
C. a<0,b<0,c<0
D. a>0,b>0,c>0
【試題答案】
一. 1. B 2 A 3 C 4 C 5 B
第一次月考【有理數的乘方】複習專練
一、填空
(1)(-4)2=__________,-42=__________;
(2)-(-4)2=__________,-(-42)=__________;
(3)(-)3=__________,-()=__________;
(4)(-2)5=__________,(-3)4=__________。
分析:(1)(-4)2表示兩個-4相乘,-42表示42的相反數,即-42=-(4×4)=-16;
(2)-(-4)2表示-4的平方的相反數,即-(-4)×(-4)=-16,-(-42)表示4的平方的相反數的相反數,即-(-42)=42=4×4=16;
(4)(-2)5表示5個-2相乘,由符號法則知,結果為負,即(-2)5=-32,(-3)4表示4個-3相乘,由符號法則知,結果為正,即(-3)4=81。
解:(1)16,-16 (2)-16,16
(4)-32,81
評析:有理數的乘方是轉化為乘法進行計算的,在計算時,一定要分清冪的底數,如:(-4)2的底數是-4,-42的底數是4,-42的意義是“4的平方的相反數”。
二、計算
(1)
(2)(-0.75)3;(3)(-1)101。
分析:把帶分數轉化成假分數,小數化為分數,再根據乘方的意義與乘方運算的符號法則進行計算。
(3)(-1)101=-1。
評析:乘方是一種積的運算,冪是乘方的運算結果,運算時,先確定符號,再算絕對值。
三、填空
分析:有理數的混合運算順序是:先算乘方,再乘除,最後算加減,有括號的先算括號裡的運算。
解:13/5
評析:本例題主要考查有理數混合運算的運算順序,以及符號的確定方法。
四、解答
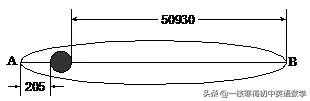
“嫦蛾一號”第一次入軌執行的橢圓軌道如圖所示,其中黑色圓圈表示地球,其半徑R=6371km,A是近地點,距地球205km,B是遠地點,距地球50930km(已知地心,近地點,遠地點在一條直線上),則AB=__________km(用科學計數法表示)。
分析:AB=205+2×6371+50930=63877(km),我們可按科學記數法的表示方法來表示。事實上,a=6.3877,然後看小數點向左移動了幾位,那麼n即為幾。
解:6.3877×104
評析:用科學記數法表示一個數時,10的指數n等於原數化為a時小數點移動的位數,n比原數的整數位數小1。
五、選擇題
下列說法中正確的是( )
A. 近似數1.70與近似數1.7的精確度相同
B. 近似數5百與近似數500的精確度相同
C. 近似數4.70×104是精確到百位的數,它有三個有效數字4、7、0
D. 近似數24.30是精確到十分位的數,它有三個有效數字2、4、3
分析:近似數1.70精確到0.01,1.7精確到0.1,故A錯;近似數5百精確到百位,近似數500精確到個位,故B錯;近似數4.70×104的有效數字只與4.70有關,與104無關,它有三個有效數字4、7、0。精確度由所得近似數的最後一位有效數字在該數中所處的位置決定,而4.70×104=47000,本題中有效數字0在47000中處在百位,故精確到百位,C對;近似數24.30精確到百分位,故D錯。
解:C
評析:(1)計算有效數字的個數時,摳住有效數字的意義,從左邊第一個不是0的數字起,到精確到的數位止,中間所有的數字,包括0,重複的數字都不能漏掉。(2)近似數後面有單位時,如百、千、萬,還有用科學記數法表示的數,其有效數字與單位無關,而精確度應該與單位統一起來考慮。
六、觀察下列算式:
31=3 32=9 33=27 34=81
35=243 36=729 37=2187 38=6551
透過觀察,用你發現的規律,判斷出3101的末位數字是__________。
分析:透過觀察,3n每迴圈4次,末位數字(個位)就出現週期變化。
當n=4k+1時,34k+1的個位數為3
當n=4k+2時,34k+2的個位數為9
當n=4k+3時,34k+3的個位數為7
當n=4k時,34k的個位數為1
而101=4×25+1,於是3101的末位數是3。
解:3
評析:由特殊到一般發現規律後,再去解決特殊的情形,這種對比發現,歸納的方法是一種學習數學的常見的思維技巧,請同學們一定要多體會、多摸索。