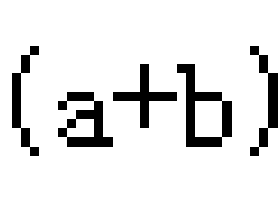奇偶判定
奇數±奇數=偶數；偶數±偶數=偶數
偶數±奇數=奇數；奇數±偶數=奇數
奇數x奇數=奇數；奇數x偶數=偶數
偶數x奇數=偶數；偶數x偶數=偶數
計算公式
平方差公式：
完全平方公式：
立方和與立方差公式：
數字變化
對任意兩數a、b，如果a－b＞0，則a＞b；如果a－b＜0，則a＜b；如果a－b＝0，則a＝b
當a、b為任意兩正數時，如果a/b＞1，則a＞b；如果a/b＜1，則a＜b；如果a/b＝1，則a＝b
當a、b為任意兩負數時，如果a/b＞1，則a＜b；如果a/b＜1，則a＞b；如果a/b＝1，則a＝b
對任意兩數a、b，當很難直接用作差法或者作商法比較大小時，我們通常選取中間值c，如果a＞c，且c＞b，則我們說a＞b
整除判定
2，4，8整除及其餘數判定法則
一個數字能被2（或5）整除，當且僅當末一位數字能被2（或5）整除
一個數字能被4（或25）整除，當且僅當末兩位數字能被4（或25）整除
一個數字能被8（或125）整除，當且僅當末三位數字能被8（或125）整除
3，9整除判定基本法則
一個數字能被3整除，當且僅當其各位數字之和能被3整除
一個數字能被9整除，當且僅當其各位數字之和能被9整除
7整除判定基本法則
一個數是7的倍數，當且僅當其末位數的2倍，與剩下的數的差為7的倍數
11整除判定基本法則
一個數是11的倍數，當且僅當其奇數位之和與偶數位之和做的差為11的倍數，則這個數就是11的倍數
工程問題
工作量＝工作效率×工作時間
工作效率＝工作量÷工作時間
工作時間＝工作量÷工作效率
總工作量＝各分工作量之和
注：在解決實際問題時，常設總工作量為1
行程問題
(1)火車過橋核心公式：
路程=橋長+車長(火車過橋過的不是橋，而是橋長+車長)
(2) 相遇追及問題公式：
相遇距離=(速度1+速度2)×相遇時間追及距離=(速度1-速度2)×追及時間
(3)隊伍行進問題公式：
隊首→隊尾：隊伍長度=(人速+隊伍速度)×時間；隊尾→隊首：隊伍長度=(人速-隊伍速度)×時間
(4)流水行船問題公式：
順速=船速+水速，逆速=船速-水速
(5)往返相遇問題公式：
兩岸型兩次相遇：S=3S1-S2，(第一次相遇距離A為S1，第二次相遇距離B為S2)
單岸型兩次相遇：S=(3S1+S2)/2，(第一次相遇距離A為S1，第二次相遇距離A為S2)
左右點出發：第N次迎面相遇，路程和=(2N-1)×全程；第N次追上相遇，路程差=(2N-1)×全程
同一點出發：第N次迎面相遇，路程和=2N×全程；第N次追上相遇，路程差=2N×全程
利潤問題
利潤＝銷售價（賣出價）－成本
利潤率＝利潤÷成本＝（銷售價－成本）÷成本＝銷售價÷成本－1
總利潤=單利潤×銷量售價=進價+利潤=原價×折扣
銷售價＝成本×（1＋利潤率）
成本＝銷售價÷（1＋利潤率）
鐘錶問題
鐘面上按“時”分為12大格，按“分”分為60小格。
每小時，時針走1大格合5小格，分針走12大格合60小格，時針的轉速是分針的1/12，兩針速度差是分針速度的11/12，分針每小時可追及11/12。
年齡問題
關鍵在於年齡差不變
幾年後年齡＝大小年齡差÷倍數差－小年齡
幾年前年齡＝小年齡－大小年齡差÷倍數差
日期問題
閏年是366天，平年是365天
其中：1、3、5、7、8、10、12月都是31天，4、6、9、11月是30天；閏年時候2月份29天，平年2月份是28天。
植樹問題
要考慮植樹的路段是不是封閉的。
封閉時：總棵樹＝總長÷間距
不封閉時：總棵樹＝總長÷間距＋1
雞兔同籠問題
注意雞與兔腿數的差別，有許多問題都可以用雞兔同籠的思想來解決，只需要列簡單的二元一次方程即可。
兔的只數=（總腳數-總頭數×雞的腳數）÷（兔的腳數-雞的腳數）
雞的只數=（兔的腳數×總只數－總腳數）÷（兔的腳數－雞的腳數）（一般將“每”量視為“腳數”）
等差數列相關公式
和=(首項+末項)×項數÷2
項數=(末項-首項)÷公差+1
從1開始，連續的n個奇數相加，總和=n×n，如：1+3+5+7=4×4=16，……
幾何問題
(1) 三角形三邊關係公式
兩邊之和大於第三邊，兩邊之差小於第三邊。
(2)勾股定理
直角三角形中，兩直角邊的平方和等於斜邊的平方。常用勾股數：(3、4、5)；(5、12、13)；(6、8、10)。
(3)內角和定理
正多邊形內角和定理，n邊形的內角的和等於：(n - 2)×180°(n大於等於3且n為整數)。
已知正多邊形內角度數，則其邊數為：360°÷(180°-內角度數)。
(4)幾何面積和體積
(5)將一個圖形尺度擴大為N倍，則
①對應角度不變
②對應周長變為原來的N倍
③面積變為原來的N*N倍
④體積變為原來的N*N*N倍
溶液問題
溶液=溶質+溶劑
濃度=溶質÷溶液
溶質=溶液×濃度
混合濃度=總溶質÷總溶液
來源： 江西公考線上
