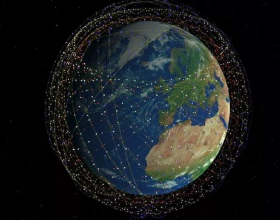
在高維空間中,有多少條線能以相同的角度成對分開?幾何學上的突破使人們對譜圖理論有了新的認識。等角線是空間中透過一個點的線,其對角都是相等的。想象一下二維的正六邊形的三條對角線,三維的正二十面體的六個對頂點的連線線(見圖)。然而,數學家們並不把假設的情況侷限於三維空間。

數學助理教授趙宇飛說:"在高維度上,事情真的變得很有趣,而且可能性似乎是無限的。但根據趙和他的麻省理工學院的數學家團隊,他們並不是無限的,他們試圖解決這個關於高維空間中線的幾何問題。這是一個研究人員已經困惑了至少70年的問題。他們的突破性研究決定了可以放置的線條的最大可能數量,以便這些線條以相同的給定角度成對分開。

Xiaodong Zhao與麻省理工學院的一組研究人員一起寫了這篇論文,這組研究人員包括本科生Yuan Yao和Shengtong Zhang、博士生Jonathan Tidor和博士後Zilin Jiang。Yao最近開始成為麻省理工學院的數學博士生,而江現在是亞利桑那州立大學的一名教師)。)他們的論文將發表在2022年1月的《數學年鑑》上。
等角線的數學可以用圖論進行編碼。這篇論文為一個被稱為譜圖理論的數學領域提供了新的見解,它為研究網路提供了數學工具。譜圖理論帶來了計算機科學中的重要演算法,如Google用於其搜尋引擎的PageRank演算法。
這種對等角線的新理解對編碼和通訊有潛在的影響。等角線是"球形編碼"的例子,它是資訊理論中的重要工具,允許不同方面在一個嘈雜的通訊渠道上相互發送資訊,例如美國國家航空航天局與其火星車之間傳送的資訊。
研究具有給定角度的最大數量的等角線的問題是在1973年P.W.H. Lemmens和J.J. Seidel的一篇論文中提出的。
普林斯頓大學數學教授諾加-阿隆(Noga Alon)說:"這是一個美麗的結果,為極端幾何學中的一個精心研究的問題提供了一個令人驚訝的答案,這個問題從60年代開始就受到了相當多的關注。"
"當時有一些好的想法,但後來人們被難住了近三十年,"Zhao說。幾年前,包括瑞士聯邦理工學院(ETH)蘇黎世分校數學教授Benny Sudakov在內的研究團隊取得了一些重要進展,當時Sudakov在組合學研究研討會上談到了他在等角線方面的工作。
Jiang在卡內基梅隆大學的前博士生導師Bukh Boris的工作基礎上受到啟發,開始研究等角線的問題。Jiang和Zhao在2019年夏天組隊,並邀請Tidor、Yao和Zhang加入。
這項研究得到了Alfred P. Sloan基金會和國家科學基金會的部分支援。Yao和Zhang透過數學系的本科生研究暑期專案(SPUR)參與了這項研究,而Tidor是他們的研究生導師。他們的成果為他們贏得了數學系的Hartley Rogers Jr. 最佳SPUR論文獎。"這是SPUR專案最成功的成果之一,不是每天都有一個長期的開放性問題得到解決的。"
解決方案中使用的關鍵數學工具之一被稱為譜圖理論。譜圖理論告訴我們如何使用線性代數的工具來理解圖和網路。圖的"頻譜"是透過將圖變成矩陣並檢視其特徵值而獲得的。
"這就像你把一束強烈的光照在一個圖上,然後檢查出來的顏色的光譜,"Zhao解釋說。"我們發現,發射的光譜永遠不可能過於集中在頂部附近。事實證明,關於圖形光譜的這個基本事實從未被觀察到。"
這項工作在光譜圖理論中給出了一個新的定理--有界度的圖必須具有亞線性的第二特徵值多重性。該證明需要將圖的頻譜與圖的小片的頻譜聯絡起來的巧妙見解。