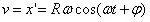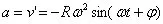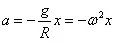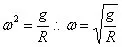突然想起個問題,如果我們從自己腳下開始向下挖,一直往下挖,直到穿過地心,到達地球的另一面,那麼從我們這裡的洞丟下一個球,這個球會怎麼樣?
顯然,這個球會一直落下去,加速落下去,不過它並不會一直加速下落,當球越過地心之後,就會受到地心對於球的吸引力,於是它開始減速,不斷減速,直到到達地球的另一面,恰好速度為0。
這真是一個完美設想,我們不需要多少的能源,就能夠將物資或者人員輸送到遙遠的地球另一面。
我們首先要解決一個問題,一個球從洞口丟進去從另一個洞口飛出來,需要多少時間?要是時間太長,挖掘穿越地心的隧道就變得沒有什麼意義。
為了計算方便,我們先做個假設,假設地球是個均勻的球體,事實上當然不是均勻的,不過按實際計算俺數學佬不會呀;我們還得做個假設,假設地球不自轉,否則考慮的變數太多,計算將變得複雜得多;最後我們還要做個假設,假設隧道中沒有空氣阻力,我們當然知道,對於十米二十米的距離,空氣阻力並不重要,對於穿越地球這麼長的距離,空氣阻力的確會產生作用。遺憾得很,我們得先不管空氣阻力了。
一開始計算,我就發現一個問題,在地球隧道中,物體受到的引力並不是固定不變的,也就是說,地球隧道中的物體運動不是勻加速運動。
以地球球心為原點建立一個座標軸,地球海平面的位置為地球半徑R,地球另一邊的海平面的位置為-R。
當小球位於海平面時,小球受到的地球引力為mg;當小球位於地球球心時,小球受到的引力為0。
用數學的語言表達這個事實,小球的位置為x時,小球的受力為f
當x=0時,f=0
當x=R時,f=mg
於是我們可以認為,當小球位於位置x時,小球受力
之所以有一個負號,是因為當小球位於x軸正半軸時,所受的引力指向負半軸,反之亦然。
這個力的表示式給了我一個很重要的啟發,似乎也有一種力也是這個表示式。對了,彈簧!彈簧的彈力f=kx,彈簧被拉得越長,彈簧的拉力越大,彈簧被壓縮得越短,彈簧的反彈力也越大。
於是,我們可以得出一個結論:小球在地球隧道中的運動,和彈簧上一個小球的運動是一模一樣的——簡諧振動。
天,原來地球引力就是一個巨大的彈簧,彈簧的平衡位置就是地心,彈簧的長度可以向兩側延伸到海平面。
好吧,我接著算下去。
小球的運動是一個簡諧運動,所以其運動軌跡
數學告訴我,位移x的導數就是速度。所以
數學還告訴我,速度v的導數就是加速度。所以
將
代入加速度,可以得到
唉。牛頓告訴我們,加速度
。所以
啊哈,我得到這麼一個結果:
三角函式的週期性告訴我,
這就是小球在地球隧道中一個來回所需要的時間,代入地球半徑R=6371km
,地面上重力加速度
得到,T≈5063秒≈84.4分鐘。
不到一個半小時,小球就能在地球隧道中打一個來回,高考數學兩個小時再加上交卷出考場時間,嗖嗖嗖,小球已經在地球隧道里跑了兩個來回。這也太快太快了吧。取半,從北半球的入口進入,從南半球的出口出來,只要42.2分鐘,哦耶!很合算呀,超音速飛機也幹不過地心穿越速度,平均速度為18000公里/小時,而一般的民航飛機時速只有600-700公里/小時,即便高效能戰鬥機,速度高達3馬赫,也就是1200+公里/小時,還需要消耗巨大的能源。
這麼大的速度對運輸的貨物或生物體有影響嗎?對於生物體的影響需要實驗,但對於貨物基本是沒有影響的,隧道中的高速不是由於超大功率發動機產生,而是重力持續加速產生,而重力對於貨物的影響就相當有限了。
地球隧道設想還有幾個問題需要解決。
隧道中的空氣阻力是個大問題。一萬公里,高速行進,空氣阻力非常驚人,尤其是隧道中,空氣受到壓迫卻無處宣洩,因此阻力更大。我們可以想象一下,如果沒有空氣阻力,一滴雨水從高空落下,速度將能夠置人於死地,但空氣起到了減緩加速的作用,使雨水落到我們身上,多數人不以為然。解決空氣阻力只有兩種辦法,一是抽真空,使隧道成為真空隧道;二是額外提供初速度,以抵消空氣造成的能量損失。當然在隧道里增加電磁線圈以加速也可以。
地球自轉也是一個問題。很顯然地球的自轉必然帶來隧道中小球的運動軌跡不是一條直徑,而是有一個弧度,儘管這個弧度不會影響週期,但不考慮自轉,隧道中下落的小球必然會與隧道壁發生碰撞。極高速度的小球與隧道碰撞,等同於在隧道內發生一次大爆炸,所以地球隧道應該是一個弧線。
地球內部的高溫高壓使得地球隧道只能是一個數學幻想。人類對於地球內部的猜想是充滿著鐵鎳高溫岩漿,其溫度之高,足以使任何生物化成一縷青煙,貨物變成一堆炭。在解決材料之前,我們玩玩數學就好。
當然了,最迫切的問題還是鑽洞問題,地球上最強悍的戰鬥民族,也不過鑽了12KM,再也鑽不下去了。
本圖不是蘇聯的鑽井,只是因為它很震撼。