一、等效法處理直線運動
處在勻強電場中的帶電體除受到靜電力外,一般還會受到重力等其他外力的作用。對於此類問題,我們可以將重力和靜電力的合力看成一“等效重力”來處理,或將重力場和電場疊加為一個“等效重力場”來處理,這樣能較簡捷地解決此類問題。
例:如圖所示,
在離斜面底端B為L的C點豎直固定一根直杆,杆高也是L。杆上端A到斜面底端B之間有一光滑絕緣的恰好伸直的輕質細繩,一電荷量為q、質量為m的圓環(可視為質點)穿過繩上,整個系統處在水平向右的勻強電場中,已知細繩與豎直方向的夾角θ=30°(取g=10m/s²)。若圓環從A點由靜止開始滑下,細繩始終沒有發生形變,求圓環在細繩上滑行的時間。
二、等效法處理類平拋問題
當帶電粒子在電場中所受合力即“等效重力”與初速度垂直時,帶電粒子運動可以看作為類平拋運動。
例題:如圖所示,
長為L的兩平行金屬板M、N傾斜放置且極板間與水平方向間的夾角為θ=37°。一質量為m、電荷量為q的帶正電小球(可視為質點)從y軸上的A點以初速度v₀水平向右丟擲,帶電小球恰好能垂直M板從中心小孔B進入兩板間。重力加速度為g,sin37°=0.6、cos37°=0.8。(1)求帶電小球從y軸上的丟擲點A丟擲時的初速度v₀;
(2)若該平行金屬板M、N間有如圖所示的勻強電場,
且電場強度大小為E=4mg/5q,為保證小球不打在N板上,求兩球平行板M、N之間的垂直距離d的最小值。
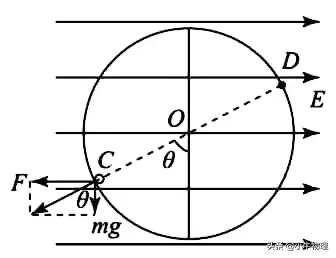
三、等效法處理圓周運動
應用“等效重力”和“等效重力加速度”求解.具體解題步驟:
1.求出重力和電場力的合力F合,這個合力視為“等效重力”mg′;
2.將g′視為“等效重力加速度”;
3.將物體在重力場內做圓周運動的規律應用到等效重力場中分析求解.
4.物理最低點.重力和電場力的合力沿圓弧半徑向外位置,即物理最低點(如圖中C 點).
a.在邏輯最低點時,帶電粒子運動的速度最大.
b.在邏輯最低點,帶電粒子對軌道的壓力最大,根據向心力公式可求得.
5.邏輯最高點.重力和電場力的合力沿圓弧半徑向內的位置,即物理最高點(圖中D 點).帶電粒子運動到最高點,“等效重力”提供向心力,臨界速度v臨=g′R.
例題:如圖所示,
絕緣光滑軌道AB部分是傾角為30°的斜面,AC部分為豎直平面上半徑為R的圓軌道,斜面與圓軌道相切。整個裝置處於場強為E、方向水平向右的勻強電場中。現有一個質量為m的帶正電小球,電荷量為q=√3mg/3E,要使小球能安全透過圓軌道,在0點的初速度應滿足什麼條件?