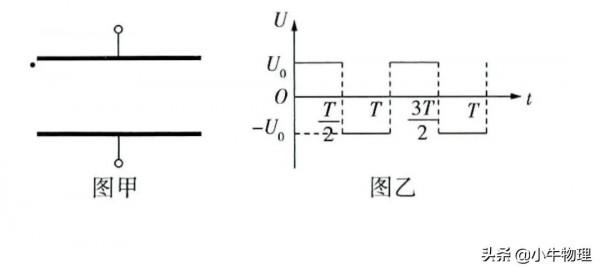
例題:如圖甲所示,兩平行金屬板水平放置,間距為d,金屬板長為L=2d,兩金屬板間加如圖乙所示的電壓(初始時上金屬板帶正電),其中U₀=16md²/qT²,一粒子源連續發射質量為m、電荷量為+q的帶電粒子(初速度v₀=4d/T,重力忽略不計),射出的帶電粒子恰好從上金屬板左端的下邊緣水平進入兩金屬板間。
(1)求能從板間飛出的粒子在板間運動的時間。
(2)在哪些時刻進入兩金屬板間的帶電粒子不碰到金屬板而能夠飛出兩金屬板間?
【解析】
(1)水平方向做勻速直線運動,t=L/v₀=T/2
(2)只要能飛出電場,時間長度一定為½T,加速度a=qU₀/md=16d/T²。
方法一:純數學分析法
設加速度向下的時間為t,則加速度向上的時間為½T-t(因為總時間為½T,加速度向下或者向上只出現一次),要從極板飛出,豎直位移要大於等於0而小於等於d,列式為
0≤½at²+[at·(½T-t)-½a(½T-t)²]≤d
取臨界解得:捨去不合理值,
t≤¼T且t≥¼(2-√2)T,
進入時間為t₁≥½T-¼T=¼T,
t₂≤½T-¼(2-√2)T=¼√2T
結合兩種情形向進行分析,進入時刻考慮到週期性,帶電粒子不碰到金屬板而能夠飛出兩金屬板間的時刻T₀滿足(¼+n)T≤T₀≤(¼√2+n)T(其中n=0,l,2,…)
方法二:v-t圖分析法
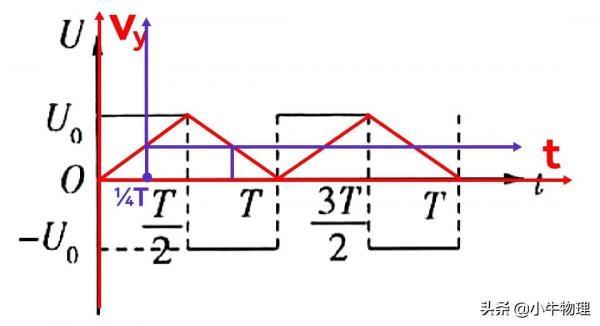
用豎直方向上的v-t圖進行分析,取向向下為正方向,先不管從什麼時刻進入的,都從0時刻進入開始分析,畫出v-t圖,如圖所示,
若從0時刻進入,時長為½T,豎直向下的位移為2d,將打在下極板上,不合題意,進入時刻必須往後推移,將座標系往右平移,進入時刻在¼T,面積恰好為d,計算過程為2×½a(¼T)²=d,則進入時刻為
t₁=¼T,如圖所示,
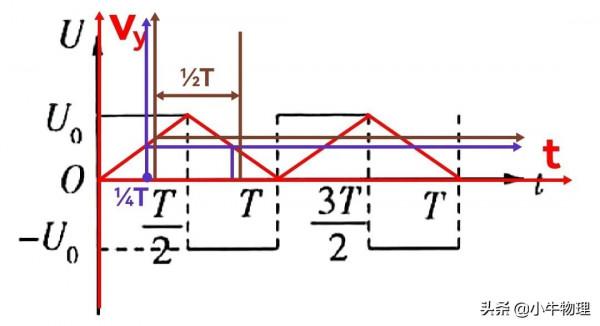
接著往右平移座標系一小段,注意時間長要保持½T,將會出現負面積,此時正面積還是大於負面積,總面積<d,能出電場,符合題意,如圖所示,
繼續向右平移座標系,當負面積和正面積相等時,即豎直位移為零,也就是剛好從上極板右端飛出,
設加速度向下的時間為t,則加速度向上的時間為½T-t
2×½at²=½a(½T-2t)²
解得t=¼(2+2√2)T
則進入時刻t₂=½T-t,t₂=¼√2T
結合兩種情形向進行分析,進入時刻考慮到週期性,帶電粒子不碰到金屬板而能夠飛出兩金屬板間的時刻T₀滿足(¼+n)T≤T₀≤(¼√2+n)T(其中n=0,l,2,…)
方法三:軌跡圖法
交變電場往往具有周期規律性,用畫軌跡的方法關鍵是找到對稱性。
0時刻進入的將打在下極板上,如圖線①所示,不合題意,因此進入時刻必須推後,軌跡將會出現拐點,如圖線②所示,直至恰好從下極板右端飛出,進入時刻繼續推後,拐點往左移動,並且還會出現豎直速度為0的另一拐點(對稱性),軌跡將往上偏移,直至恰好從上極板右端飛出。如圖線③所示。
恰好從下極板右端飛出,速度水平且為v₀,由對稱性,顯然可知粒子在電場中運動時間為¼T,進入時刻為t₁=½T-¼T=¼T。
恰好從上極板右端飛出,在第一個半個週期內,設帶電粒子在t₂時刻進入兩金屬板間,它在豎直方向上先加速向下,經過t時間後電場反向,開始在豎直方向上減速向下,又經過時間t,豎直分速度減為零,然後加速向上,經過時間½T-2t直到恰好從上金屬板右端飛出,畫出其運動軌跡,如圖所示。
找到電場方向相反的兩個對稱時間,這樣豎直速度就會為零。
從右端飛出,豎直位移為零
2×½at²=½a(½T-2t)²
解得t=¼(2+2√2)T
則t₂=½T-t=¼√2T
結合兩種情形向進行分析,進入時刻考慮到週期性,帶電粒子不碰到金屬板而能夠飛出兩金屬板間的時刻t滿足(¼+n)T≤T₀≤(√2/4+n)T(其中n=0,l,2,…)