無窮大與無窮大，誰大？

❝

前言

看到這個標題，大家是不是覺得很奇怪呢？無窮大就是無窮大，怎麼無窮大還能分個三六九等？

然而數學有的時候不一定跟著直覺走。很多時候，經過嚴格的推理和論證，我們可以得出很多反直覺，但確實正確的結論。

在數學上，關於無窮大的討論，人們曾經經歷了很多的爭論，甚至還把相關理論的發明人，數學家康托爾，逼到精神失常。所幸，現在這個爭論終於塵埃落定，現代數學關於無窮大已經有了一套比較完備的理論。姑且寫出來，分享之。

❞

神奇的希爾伯特旅館

希爾伯特旅館是數學上一個著名的思想實驗，也是關於無窮大的理論的基石。或許不少看到這篇文章的小夥伴之前都聽過。不過我這裡，還是覺得以這個引入是最好的，所以這裡就再寫一遍咯。沒接觸過的小夥伴正好來看一下~

設想有一個無限大的旅館，裡面有標號1,2,3...的無窮多個房間。現在，所有的客房都有客人了。考察下列情景：

某天，張三帶著他朋友們組成了一個10人旅行團來這裡旅遊，想要住這個旅館，請問能不能給他們安排房間？

第二天，張三僱了一輛無窮巴士，帶來了標號1,2,3...的無窮多個朋友來這裡旅遊。請問，能不能把他們都安排上房間？

第三天，張三找了一個無窮旅行社，從裡面僱了編號1,2,3...的無窮多個巴士，每一個巴士上都有標號1,2,3...的無窮多個客人。請問，能不能把他們都安排上房間？

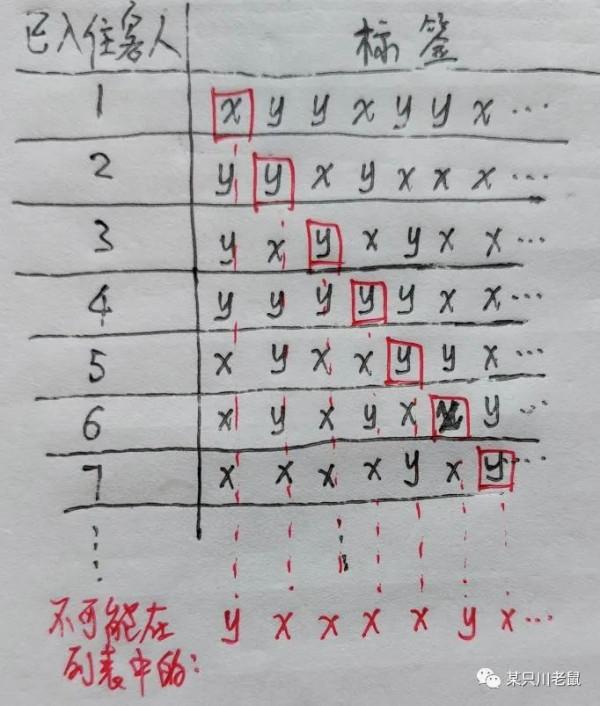
第四天，張三找了一輛“超級無窮巴士”，上面的客人不用1,2,3...編號，而是每人身上都貼著一個標籤，標籤上寫著只包含"x"和"y"這兩個字母的無限長的字串。假設每個人身上的標籤組合起來，可以包含所有由"x"和"y"這兩個字母的無限長的字串組成的字元，並且不同人對應的字元各不相同。請問，此時還能給這些人安排房間嗎？

正確答案是：前三天都可以，第四天這個旅館就歇菜了。

第一天，只要讓編號的房間裡的客人移動到第號房間去住，前10個房間就騰出來了。

第二天，把所有正整數分成奇偶兩組，讓編號為的房間裡的客人移動到號房間去住，然後讓第個客人住第號客房即可。

第三天，還是先讓編號為的房間裡的客人移動到號房間去住，把1,3,5,7,9...號客房騰出來。我們把第個巴士上的第個客人記作。那麼，讓（即）住第1號客房，讓（即）住第3,5號客房，讓（即）住第7,9,11號客房，讓（即）住第13,15,17,19號客房……如此繼續下去，按照的值從小到大的順序一組一組安排，總能把所有客人安排進去。

然而到了第四天，事情就不對勁了。假設我們把所有的客人都安排進去了。現在，考察這麼一個客人，對於任意正整數，他身上對應的字串的第位和第名已經入住酒店的客人的第個字元不相同（也就是如果入住的客人的那一位是x，他就取y，反之亦然）。這樣一來，這個客人的字元就和每一名已經入住的客人的。從而，這個客人沒有入住，這和我們的假設“所有客人都安排進去了”矛盾。藉助反證法的思想我們知道，這個旅館第四天必須掛出“今日滿員”的牌子。

下面的圖可以幫助大家理解第4天發生的事情：

無窮大到底怎麼比大小？

一一對應原則

從上面的例子可以看到，無窮大之間比大小，就不像有限量比大小一樣，”我比你多我就比你大”，而是要藉助其他的原則。

這個原則是什麼呢？

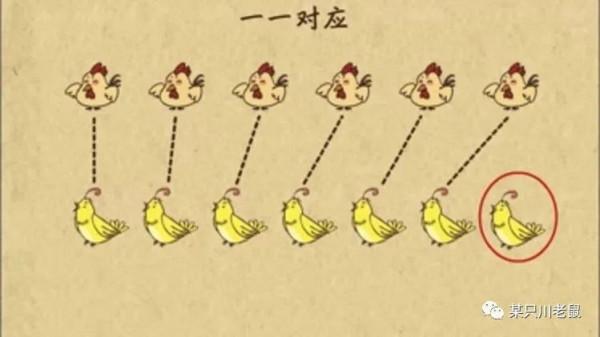
我們還是從有限量的比較獲得靈感。假設一個劇場有1000個座位，你一上臺發現臺下既沒有沒人坐的空位，也沒有人坐在臺階上這種“不該坐”的地方，並且每個座位上都只有1個人，沒有家長抱著小孩坐這種情況。請問：臺下有多少觀眾？

大家一定可以立刻回答出來：1000個。那麼，為什麼可以立刻回答呢？

顯然，在這個場景下，觀眾和座位形成了一一對應，因此它們的數量也一定是“一樣多”。

在數學裡，無窮大的比較遵循的是一樣的標準：一一對應。如果兩個無窮集合裡面的元素可以形成一一對應，那麼這兩個集合的元素個數就是“一樣多”。如果無窮集合A可以和無窮集合B的一個子集的元素一一對應，但集合A卻無法和集合B中的所有元素進行一一對應，那麼就說集合B的元素比集合A多。

一個重要的定理

現實情況下，一一對應的規則往往不好構建，很多時候我們都只能構建一個集合到另一個集合的子集的對應規則。那麼，設有兩個無窮集合，如果我們構建了法則可以把一一對應到，又構建了法則可以把一一對應到，那麼，A和B之間是否存在一一對應呢？

答案是：一定存在。我們甚至可以直接把這個規則寫出來：

為方便起見，我們現在把和分別寫作和。設。根據定義，，。我們再對和使用法則，設，。由於，而是一一對應法則，根據和可知：。同理，。而這兩條，就可以看做和之間的一一對應法則。

現在，重複上述操作，定義，再定義，。同理可得，，。而這兩條，就可以看做和之間的一一對應法則。

如此繼續下去，我們可以得到和之間，和之間。。。的對應法則。而我們的集合構建規則是和，。從和，藉助和為一一對應這一特點，用數學歸納法容易證明：和。從而，將我們構建的對應規則綜合起來，就形成了（即）到（即）的一一對應規則。

如果上面的表述太數學化，下面的草圖可以幫大家理解：

圖中，相同紅色數字標出的小段之間具有一一對應關係，對應法則我已經在後面用字母標出。

可見，如果我們可以構建兩個法則，分別把兩個無窮集合對應到對方的一個子集，我們也可以說這兩個集合的元素個數“一樣多”。

無限集的勢

對於有限集，元素的個數可以用一個正整數來表示，而對於無限集，這顯然不行。而我們從希爾伯特旅館中可以看到，無限似乎又是可以比較大小的。所以，對於無限極的數量，我們必須給它一個名字。這個名字就叫做無限極的勢。數學上，常用符號（讀作“阿列夫數，Aleph數”）表示。

根據一一對應規則，如果某兩個集合的元素“一樣多”，就說它們的“勢”相等，或它們“等勢”，即。如果A比B元素“多”，就說A的勢比B大，即。

這樣，之前證明的定理就可以表示為：如果兩個無窮集合A和B可以和對方的子集一一對應，那麼必有。這個定理叫做Bernstein定理。

最小的勢：

在所有無限集中，顯然大家能想到的元素數“最少”的就是正整數集。這是因為，既然要無限，至少至少，元素必須能一個一個排起來，一直排下去。那麼，對於這個集合，我們就把它的勢記作。這是所有的勢當中，最小的一個。

那麼，根據一一對應的規則，任意可以和一一對應的無限集的勢必然都是，其個數和“全體正整數”的個數一定一樣多。這樣的集合我們稱為“可數集”，這樣的元素個數我們稱為“可數”。

下面，我們要開始證明一些重要的結論了。提醒：有些可能會反直覺哦。

結論1：

很簡單，將全體整數按照0,1,-1,2,-2,3,-3,4,-4...排列，並分別對應1,2,3,4,5....即可。

但是，我們知道，。從而，這個簡單的例子告訴大家一個很重要的事情：無窮集完全可以和自身的真子集一一對應！。這在有限集裡面顯然是不可能的，但是一旦我們討論“無窮”，事情就不一樣了！

結論2：

什麼？！有理數？！您沒騙我？！有理數那麼多，居然和正整數個數一樣多？！

我們來看：現將有理數按照

這樣排列。按照第一行，第二行，第三行。。。這樣的順序依次寫下有理數，並且剔除掉和前面的值有重合的元素(例如保留而剔除)，我們就把有理數排成了一列，然後將這一列按次序分別對應1,2,3,...即可。

很反直覺，但是無懈可擊。

結論3：設為（可數）無限多個有限集，且有無限多個元素。則

很簡單，將中的元素順次排列，剔除重複元素，再按照排列次序與對應即可。

結論4：設為一列無限集，且。則

證明：考察希爾伯特旅館第三天的情況。既然，集合中的元素一定可以和第輛無窮巴士中的乘客一一對應，而還要剔除可能存在的在不止一箇中出現的元素。因此，顯然可以和“全體無窮巴士中全體乘客”這個集合的一個子集對應。而希爾伯特旅館第三天的情況已經證明，“全體無窮巴士中全體乘客”可以和集合{1,3,5,7...}一一對應，集合{1,3,5,7...}又顯然和{1,2,3,4...}可以一一對應（這個太明顯了）。從而，“全體無窮巴士中全體乘客”可以和一一對應。所以，可以和的一個子集一一對應。

另一方面，顯然可以和的一個子集對應，取任意一個作為這個被對應的子集即可。從而，根據Bernstein定理，。

所以說，即使把可數個可數集的元素全湊在一起，全體元素的個數依然可數！類似地，有限個可數集的並集依然可數，就很顯然了。

結論5：代數數集可數

代數數的定義是：可以成為整係數多項式方程的根的數。有理數自然不必說，*很多無理數也屬於代數數，例如，等。*那麼，為什麼代數數集也可數呢？

我們知道，任何整係數多項式方程的根的個數都是有限個，但是整係數多項式方程有無限多個。如果可以證明整係數多項式方程的個數是可數的，那麼每個整係數多項式方程的解顯然是有限個，根據結論3就完成了命題的證明。

由於整係數多項式方程顯然和有序有限項整數數列一一對應（直接去從高次項到低次項的係數即可，數列項數=多項式次數+1），我們只需證明：全體有限項有序整數數列的個數是可數的。

設為全體“含有項的有序整數數列”構成的集合，。顯然，“全體有限項有序整數數列”構成的集合就等於。因而，如果能證明對任意正整數，可數，根據結論4就相當於證明了全體有限項有序整數數列的個數是可數的，也就相當於完成了命題的證明。

如果我們定義集合，來表示“全體n項有序整數數列中絕對值最大的項的絕對值等於構成的集合，那麼顯然為有限集，且。從而根據結論3，知可數。這樣，我們就完成了命題的證明。

更高階的勢：

無理數比有理數多嗎？

在希爾伯特旅館中，我們已經看到，旅館在第4天就不得不掛出滿員的牌子。這說明，第4天的那個“超級無窮巴士”裡面的乘客數比全體正整數的個數要多，也就比我們剛才所有提到的集合元素個數都要多。

那麼，這個“超級無窮巴士”到底有多少乘客呢？

首先，我們做這麼一件事：給“超級無窮巴士”上的每一位乘客都改個名字。把所有乘客的標籤上所有的x都改成0，y都改成1。接著，我們在每個乘客前面都加一個“0.”。這樣一來，'xyxxyyyy...'就成了'0.0100111...'，'yxyxyxyx...'就成了'0.10101010...'，如此等等。

如果我們把改名之後的東西看成二進位制小數，我們就不難發現，全體“超級無窮巴士”上的乘客，就對應於全體以'0.'開頭的二進位制無限小數的集合，而這就對應了之間的全體實數！【注：有理數可以寫成無限迴圈小數，有限小數我們也改用迴圈小數表示，例如0.101可以表示為0.100111111....（1無限迴圈)】

因而，我們可以說，“超級無窮巴士”上的乘客的個數，就是之間全體實數的個數。根據下面的對應規則，我們可以構建至的一一對應關係：

而與此同時，函式又可以完成至的一一對應。因此可以說，“超級無窮巴士”上的乘客的個數，也等於全體實數的個數。

當然，只要我們藉助二進位制小數，把希爾伯特旅館第4天中那些人的標籤上的x和y分別換成0和1，很容易證明，實數的個數比有理數多。

那麼這個個數如何理解呢？我們現在再換一個角度去看看那些二進位制小數。如果我們把開頭的'0.'給去掉，每一個二進位制小數就成了一個'0'和'1'構成的無限長序列。而如果我們現在再把搬出來，並且寫出其全部的子集，這個子集能否和這些序列一一對應呢？

當然可以，而且對應規則很簡單！給定一個序列，在第幾位取到1，我們就去正整數集中的第幾個元素放到子集裡。從而，序列“1011011..."對應子集{1,3,4,6,7...}，序列“000100101101..."對應子集{4,7,9,10,12...}，如此等等。原來，上的全體實數（因而也可以說整個實數集中的實數），根本就可以和的子集一一對應！

我們知道，元素有限集的子集個數為。因此，這裡我們不妨沿用這個記號，把全體實數的個數記作。數學上，我們常常將它寫作：。

可見，，從而實數比有理數多。這也就說明無理數一定比有理數多，否則如果有理數和無理數一樣多，二者都可數，它們的並集也一定可數（前面已經證明），這就和矛盾。

無理數比有理數多很多嗎？超越數比代數數多很多嗎？

剛才，我們看到，實數比有理數多，從而無理數比有理數多。那麼，這個多，是多多少？多一點還是多很多？

我們來看下面這個實驗：既然有理數可數，我們可以把它們寫成。設數集

其中。顯然，。另一方面，的長度顯然不超過各區間長度之和：

而可以取任意正數。這就說明，我可以用總長度任意小（可以任意小）的一個數集，把全部有理數都覆蓋住。然而，整根實數數軸的長度是無限長！由此，實數不僅比有理數多，而且比有理數多很多！那麼，自然地，雖然有理數和無理數在實數軸上都是稠密的，也就是任意小的區間裡面都有無窮多個有理數和無理數，但有理數的個數和無理數相比嘛。。。大概就是。。。

同樣的道理，我們把這個過程擴充套件到複數平面上，把小區間換成小圓圈，可以證明：超越數不僅比代數數多，而且比代數數多很多！

所以說，數學是非常神奇的。我們現在已經知道無理數比有理數多很多，可是當年無理數的發現者希帕索斯卻被扔進了大海。我們現在知道超越數比代數數多很多，可是證明諸如，這樣的數是超越數可絕非凡人能做。這，可能就是數學讓人神魂顛倒的地方吧。

是無窮大的“天花板”嗎？

從剛才的實驗中，我們已經感覺到，比要大很多。那麼，這是“無窮大”個數的天花板嗎？

考察一個無限集，定義其冪集為的全體子集的集合，即：

顯然，集合和集合中元素可以一一對應，而同樣顯然的是，。因此，。而下面的這個定理，直接否定了取等於號的可能性：

任何無窮集合和它的冪集中的元素不可能以任何方式構成一一對應關係。

證明：設某集合的元素和它的冪集的元素之間構成了一個一一對應關係。設集合。設（由於為一一對應，顯然存在逆向規則，且t在S中）。那麼，如果，則由知，直接違背的定義，從而。而如果，又同時滿足了（打錯，這個T應為S）和兩個條件，完全符合的定義，從而。怎麼都矛盾，只能是假設出錯，從而無窮集合不可能和其冪集之間存在一一對應關係。

這樣一來，即使我們從可數集開始，也可以透過構建冪集，冪集的冪集，冪集的冪集的冪集。。。。一直套娃下去，這些集合的勢也一定會越來越大。套娃無止境，勢就可以無限發展，沒有頂棚。

仿照和的關係，我們不妨寫出一些列的勢：，，。。。。一直下去，永無止境。而至於這些勢中間有沒有夾著別的勢，數學家已經證明，以現有的公理體系，既無法證明這個命題，又無法證偽。

一些關於無窮的有意思的數學問題

說到這裡，可能大家已經被“無窮大”這麼一個神奇的東西迷住了。實際上，“無窮大”在數學中的確是一個神奇的玩意兒。

這一節的內容，其實和上面沒什麼關係。但我決定放在這裡，就是通過幾個由易到難的和無窮大相關的問題，提醒大家，一旦涉及到無窮，即使是可數無窮，很多時候它甚至不是有限的情況的“極限”，而是可能和“有限”的性質完全不同。一定不能憑藉直覺來判斷！

有理數相加

有限個有理數相加一定是有理數嗎？（可數）無限個有理數相加一定是有理數嗎？

相信這個問題很簡單：有限個有理數相加相當於有限個分數相加，咱大不了通分，總能把最終結果寫成兩個整數的比值。但無限個有理數相加，我們直接看下面的例子就好：

左邊=無理數，右邊=無限個有理數相加，嘖嘖嘖。

集合列交集

已知有（可數）無窮多個滿足下列條件的數集：

每一個都含有不可數無窮多的元素

那麼，

對任意正整數，交集中是否一定包含無窮多個元素？
交集中是否一定包含無窮多個元素？

看起來，第二個問題不過是第一個問題的極限情況，但正確答案是：第一個是一定的，第二個就不一定了。

當有限時，根據這一關係，容易得出。又因為每一個都含有無窮多的元素，所以取，顯然也應該有無窮多個元素。

但是如果我們取所有集合的交集，情況就不一樣了。例如：取。顯然，這一列集合同時滿足上面兩個條件，但對於任意實數，總能找到使得。從而，（空集）！不僅不包含無窮個元素，而且是一個元素都沒有！

小球入箱

設有一個無限容積的箱子和無窮多個標號為#1,#2,#3...的小球。第一次操作，將#1至#10號小球放入箱子，然後隨機從中選擇一個小球拿出來。第二次操作，將#11至#20號小球放入箱子，然後隨機從箱子裡剩下的（19個）小球中選一個拿出來。第三次操作，將#21至#30號小球放入箱子，然後隨機從箱子裡剩下的（28個）小球中選一個拿出來。就這樣重複下去。顯然，經過任意有限次操作，箱子裡剩下的小球數和一共放進去的小球數量之比嚴格等於9：10。

那麼，給定一個小球，它經過經過（可數）無限次操作後，留在箱子中的機率是嗎？

正確答案：不是！

我們來看一看：我們假設考察的小球是在第k次操作被放入的。則，放入後箱子裡應該有個球。從而，小球第一次留下的機率就是。同理，第次操作，我們是個小球中隨機拿出一個，所以小球留下的機率是。以此繼續往下，每次小球留下的機率是，... 從而，無限次操作後，小球留下的機率就是：

一直這樣乘下去，乘無限次。

我們知道，是一個隨正整數遞增的序列。因此，

這就說明，

。同理，我們也可以得到

，

，等等。從而：

對於括號裡的東西，顯然分子分母中的，等可以相互抵消，經過無窮項相乘，最後的結果就是

看看，即使箱子裡的小球的個數一定是越來越多，但是經過無限次操作，任何給定小球終將被取出。這就是數學。