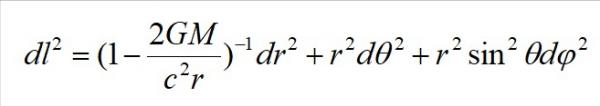如果問你最早接觸的數學常數是啥？想必很多人都會脫口而出：圓周率！

沒錯，圓周率在小學期間就已經被我們所熟知，簡單來講，不論是多大面積的圓，它們都有一個共同點，那就是周長與直徑的比值都為一個常數，這就是圓周率π，而且它還是一個無理數，也就是無限不迴圈小數。

圓周率歷史

數學史上有很多關於計算圓周率的記載，對於我們來講，最熟知的莫過於“祖沖之計算圓周率”，這位南北朝時期的數學家，第一次將圓周率精確到小數點後7位，並且這一記錄領先了西方近千年之久。

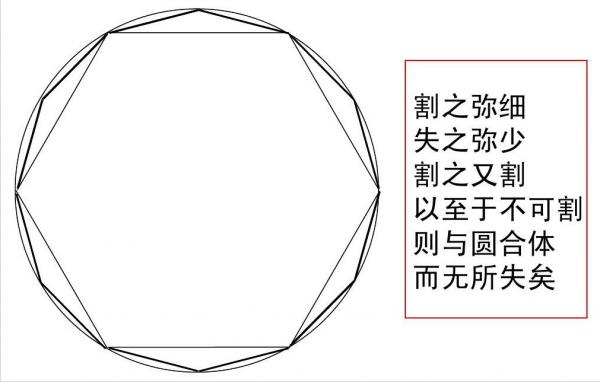
不過我們感興趣的是祖沖之是用的什麼辦法去求的圓周率呢？實際上，他所用的辦法正是魏晉時期的大數學家劉徽所提出的“割圓術”，其書中的原話是：“割之彌細，所失彌少，割之又割，以至於不可割，則與圓周合體而無所失矣”。

簡單來講就是用一個多邊形去逼近圓形，多邊形的邊越多，那麼就越接近圓（以現代的眼光看來，其本質就是微積分中的極限思想）。

割圓術本質上是一種幾何法，但隨著數學的進步，出現了更為方便精準的分析法，比如無窮級數等，給出了很多圓周率數值表示式。

再往後隨著計算機的出現，圓周率計算的位數更是直接呈幾何式的翻倍。

比如在2021年8月5日，瑞士的科研人員宣佈他們利用一臺超級計算機，耗時108天零9個小時，算出了圓周率小數點後62.8萬億位，這是一項新的世界記錄，不過他們也表示，這項紀錄可能不會保持太久。

因為在此之前的2020年以及2019年，分別有人創造了50萬億位和31.4萬億位的記錄。2020年的是由一位愛好者利用個人電腦，耗時303天，算出了50萬億位。而2019年的是由谷歌雲計算系統耗時121天，算出了31.4萬億位，準確來說是小數點後 31415926535897 位，目的為了紀念那年3月14日的國際圓周率日。

為何要算那麼多？

如果說古時候的數學家計算圓周率是為了尋找更多數學性質，畢竟那時候的數學遠不及現在豐富深厚。但是自從1761年，德國數學家蘭伯特證明了圓周率為無理數（也就是無限不迴圈小數）。

以及1882年，也是德國數學家林德曼證明了圓周率為超越數（即不能作為有理係數多項式根的實數，由此可以知道古希臘時期，想靠直尺和圓規完成“化圓為方”是不可能的）之後，似乎再瘋狂追求圓周率的位數就成了一件無用的事情？

但自從計算機出現後，人們對於圓周率位數的計算反而更加“瘋狂”了，為何呢？難道是因為圓周率越精確，越有利於科學研究或者實際生活使用？並不是，實際上圓周率用到幾十位，就已經非常精確了。

但人們還一直計算圓周率的原因，其實很簡單：能在更短時間內算出更多的位數，這種高精度的計算是判斷一臺計算機處理能力是否優秀的手段之一。

若能算盡，會發生啥？

如果圓周率哪一天被證實能算盡了，會發生啥事呢？估計不少朋友都曾想過這樣的問題。

但實際上，在通常情況下，這種情況是不會出現的，因為圓周率是無理數這一結論是透過嚴格的數學證明給出的，拔出蘿蔔帶出泥，如果圓周率真被算盡了，那將是數學大廈的一場大地震。（考慮到數學不同於自然學科，它不需要對應客觀世界的實體存在，也就是說，數學是一個放之四海而皆準的東西）

但是請注意，這個結論有一個前提，就是上段頭所言的“通常情況”，那麼這個通常情況到底是個啥呢？

• 歐氏與非歐幾何

很簡單，我們現在所熟知的圓周率數值3.14159......，實際上是建立在歐幾里得幾何體系之內的。

啥是歐幾里得幾何？很簡單，就是我們中小學時期所學的幾何，比如過直線外一點，只能做出一條平行線（平行公設）

再比如，三角形內角和為180度等等，有這些結論的都是歐幾里得幾何。

但隨著數學的發展，人們發現，這種幾何體系雖然和現實世界十分相符，但似乎並不唯一，於是人們就以剛才那條平行公設為切入點，又發現了兩種新幾何（非歐幾何），分別是羅氏幾何和黎氏幾何，在這些幾何當中，三角形的內角和不再是180度、圓周率也不再是一個固定值了。

後來經過黎曼的努力，三種幾何統一成了黎曼幾何，這也是後來愛因斯坦的廣義相對論所要用到的數學理念。

為了形象地介紹在不同幾何環境下，圓周率的變化，下面就以相對論為背景，來說明這個問題。

• 愛因斯坦轉盤內的圓周率

1909年，愛因斯坦的好友保羅·埃倫費斯特在《物理雜誌》上發表了一篇簡短地只有兩面紙不到的論文，標題為《剛體的勻速轉動與相對論》（注意，此時廣義相對論還沒問世，只有狹義相對論）。

論文提出了這樣一個“簡單”的問題：如果有一個勻速轉動的圓盤，我站在外面用量尺去測量圓盤周長，以及站在圓盤上用量尺去測量圓盤周長，試問結果如何？

這個問題看上去非常簡單，根據狹義相對論，運動的物體會在運動方向上收縮，也就說如果在圓盤靜止時，在其周邊擺放上一圈量尺（比如一根量尺長度一釐米，就這樣擺一圈，當然了，量尺越短越好，因此那樣就無限逼近圓形周長了），之後圓盤勻速轉動，由於運動尺縮，圓盤上原本首尾相連的量尺，竟然出現了空隙，而圓盤的周長是由量尺數量決定的，因此這也就說明圓盤周長變長了。

注意，上面這段話是比較籠統的說法，用於科普是沒有問題的，細究的話還要細分，不過最後的結論是正確的，也就是轉盤系測量的周長要大於地面系。（如果有了解相對論的朋友，應該對於下面給出的空間線元不陌生，這就是結論的依據）

這時候我們發現，圓盤周長變長了，但直徑卻沒有變化，那豈不是說圓周率變大了嗎？而且圓周率的數值與轉盤速度掛鉤了，理論上，圓周率直接可以變為整數！不過這沒有什麼好奇怪的，因為轉盤空間已經不符合歐氏幾何的要求，而是屬於非歐幾何了。

• 彎曲時空下的圓周率

實際上，按照廣義相對論的要求，我們現實世界中的圓周率其實原本就不是3.14159......這樣的數值，因為現實世界很難找到嚴格意義上的歐氏空間，但凡空間裡存在一個物體，那麼就不屬於歐氏空間了。

原因很簡單，因為廣義相對論將引力解釋為時空彎曲，以最簡單的史瓦西時空而言，單獨把空間線元拎出來，你會發現它長下面這個模樣

很明顯，如果畫一個圓，其半徑方向上的空間是非歐的，也就是半徑是個變數，與引力源的質量能量分佈相關，由此可見，圓周率自然也是一個變量了。

總結

由此可見，歐氏幾何中的圓周率是不能被算盡的，是一個無理數，如果能被算盡，只能說明我們現在用的數學體系要修改了。

而在非歐幾何中的圓周率則大有不同，能不能算盡，得看具體情況，總之這就和非歐幾何中三角形內角和不為180度一樣，熟悉之後，也就沒什麼好奇怪的了，更不會發生啥事。而且依據廣義相對論，非歐幾何才符合真實宇宙，而歐氏幾何只是非常接近於真實宇宙而已。