說明:本文95%以上摘錄自葛雲保先生的科普書《誰見過地球繞著太陽轉》
喜帕恰斯(又名伊巴谷)是古希臘偉大的天文學家,由於年代久遠,他的著作沒有流傳下來,現在所知的關於他的工作都是從托勒密的著作中得來的,我們不清楚他的生平,只知道他生活在公元前2世紀。他對天文學有許多傑出的貢獻,我們不在此一一列舉,僅舉兩例,來領略一下這位天才的眼光和智慧。
前面我們說過,要想知道一個月到底有多少天,就得去數,如從滿月數到下一次滿月。什麼時候是滿月呢?有人會說,就是月圓的時候唄,但什麼時候月亮就圓了呢?僅憑肉眼,別說是確定月圓的準確時刻,就是確定月圓在哪一天也不容易,十五、十六的月亮看上去都差不多圓。當然天文學家知道,只要仔細測量太陽和月亮所在的經度,等它們相聚180度時,就是月圓的準確時刻。有了準確時刻就可以開始數了嗎?是的,但是一個人一輩子最多也就數上三四十年,要想得到更精確的數值就困難了,因為我們知道,數的時間越長,平均值就月精確,這個方法適用於所有的週期運動。為了能夠得到更精確的數值,天文學家可以一代接一代地數下去,數上個三四百年怎麼樣?那精確度應該可以了吧,但是這種數法就顯得太麻煩,也太不聰明瞭。
到了喜帕恰斯生活的時代,天文學家已經知道月食形成的原因,當日、地、月三者完全在一條直線上的時刻,地球擋住了太陽射向月球的光,於是發生了月食,月食時刻就是精確的滿月時刻,不難理解,任意兩次月食之間相隔的月數一定是整數,所以從某一次月食發生的時刻數到另一次月食發生的時刻,不是很好嗎?怎麼以前就沒人想到這一點呢?
喜帕恰斯把自己非常精確的月食觀測記錄和巴比倫流傳下來的月食記錄進行對比,選擇兩次有代表性的月食,這兩次月食相隔4267個月,總共是345個埃及年(古埃及曆法每年365天)再加82天再加1小時,即126007天又1小時,那麼,用126007.04除以4267個月,就得到平均每個月是29.53059天,這個數值和今天的精確值相比,只是小數點後面第五位有微小誤差。你看,這是多麼讓人叫絕的聰明做法!
2009年7月22日,中國的中部地區發生了一次日全食,安徽的安慶、銅陵處於日食帶的中心位置,都看到了日全食,而在安慶、銅陵的正北方的北京市則同一時刻看到了日偏食,當月亮遮住太陽最多的時候,太陽直徑的約4/5被擋住了。
你覺得這些資料對你有什麼意義嗎?你由此想到什麼了嗎?公元前2世紀的喜帕恰斯也遇到過一次日全食,有一天在土耳其附近發生了日全食,而同一時刻,在埃及的亞歷山大城,看到的是日偏食,太陽的直徑最大被遮住4/5。作為天文學家的喜帕恰斯敏銳地捕捉到這一重要資訊,因為這等於是測量到了月亮的視差,儘管這種測量比較粗糙。
什麼叫“視差”呢?這兒需要解釋一下天文學中經常會提到的“視差”概念及其運用。
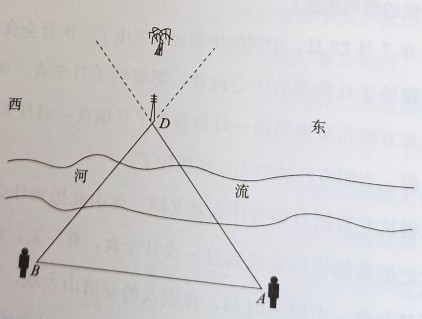
人站在一條河的南岸,想要測量北岸的電杆離自己有多遠,有什麼辦法呢?如下圖所示,人站在A點觀測河對岸的電線杆D,覺得電杆後面的大樹在電杆的東側;當人走到B點時,再觀測電杆D和大樹,大樹移到電杆的西側了。大樹和電杆的視位置發生了變化,這就是視差。要想測量A點到D點的距離,人無需跑到河對岸去,只需測出A、B兩點之間的距離,再測出角A和角B的度數,就可以根據這三個資料畫出一個與實際情況完全相似的三角形,根據三角形的特性,就能計算出A點(B點也一樣)到D點的距離。天體離我們非常遙遠,我們無法直接丈量,而幾何學給我們提供瞭解決辦法,使我們可以飛越千萬裡去丈量天體與我們的距離,這就是天文學中,尤其是早期的天文學中經常運用到的視差測距方法,後面我們還會經常提到它。
有了月亮的視差,喜帕恰斯就能計算出月亮與地球的相對距離是多少,據說證明與計算過程是這樣的。
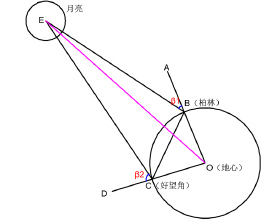
如圖6.10所示,B點為土耳其附近的達達尼爾海峽,在那兒看到了日全食,A點為埃及的亞歷山大城,在那兒看到了日偏食,太陽的直徑最大被遮住4/5。地球上看太陽的視直徑是0.5度,在A點看到太陽直徑的1/5(圖6.10中CD),所以視角CAD=0.1度,從圖6.10中看出,角BEA=角EDA+角EAD(三角形外角等於兩個不相鄰的內角的和),由於太陽相比月亮離我們遠得多(古希臘人認為是20倍左右,實際是近400倍,圖6.10無法按實際比例畫出),所以角EDA遠遠小於角EAD,因此角BEA可以看成近似等於角EAD,即等於0.1度。因為月地距離非常遙遠,所以EA和EB也可以近似為相等。
這樣,三角形EBA就是一個等腰三角形,我們知道了它的頂角等於0.1度,那麼只要再知道底邊A、B兩點的距離,就可以算出EA(或EB)的長度。喜帕恰斯根據兩地的經緯度資料,算出了達達尼爾海峽和亞歷山大城間的距離約為地球周長的1/40(因為兩地幾乎在同一經度,所以只需要測出兩地的北極星高度差,就能算出兩地的緯度差為9度,即兩地的圓心角為9度),於是求出月地距離約為地球半徑的90倍。
圖中O點是地心。地球上A點的緯度等於角AOC,A點看到的北極星在Ab方向,Aa連線是A點處的地平線,角aAb是A點處北極星高度,很容易測量出來,因為Oc垂直Aa,所以角aAb=角AOC,即北極星相較A點地平線的高度正好等於A點處的緯度值;同理,角dBe是B點處北極星高度,角dBe=角BOC,B點北極星的高度也等於B點處的緯度值。所以A、B兩地的同心角等於兩地的北極星高度差。
這種測量與計算是粗糙的,但這種眼光確是天才的。據說喜帕恰斯後來又把其中的資料做了精心調整,重新計算,得到月地距離是地球半徑的59~67.3倍。
後來喜帕恰斯又透過觀測月亮在兩個不同緯度地方的地坪高度,得出月亮的距離約為地球直徑的30又1/6倍,這個數值比實際稍小一點。
好了,這一講就到這裡了。
我是科學發現之歷程,一個致力於科普數學、物理的科技媒體。想了解更多相關的知識,關注微信公眾號科學發現之歷程,期待你的到來~