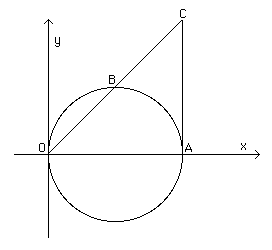將立方體加倍

後來的評論員對這個問題是如何產生的，有兩種不同的說法。士麥那的底座引用作品埃拉託斯提尼

埃拉託斯提尼在他的著作“普拉託尼克斯”中提到，當上帝透過神諭向德利安人宣告，為了消除瘟疫，他們應該建造一座比現有聖壇高出一倍的祭壇時，他們的工匠們陷入了極大的困惑，試圖發現如何將固體變成類似固體的兩倍；因此，他們去問。柏拉圖關於這一點，他回答說，神諭的意思不是說神想要一座兩倍大的祭壇，而是希望在給他們佈置任務時，使希臘人蒙羞，因為他們對數學的忽視和對幾何學的蔑視。

瘟疫無疑是雅典歷史上的一件大事，大約四分之一的人口死於瘟疫。這是在附近430因此，如果這個故事中有任何真相的話，我們至少可以給出一個合理準確的出現問題的日期。這也與以下方面的早期貢獻相一致：希波克拉底解決問題。但是，有一個問題是柏拉圖因為他直到出生427公元前。

尤託修斯，在他的評論中阿基米德' 關於球體和圓柱體給出了一個有點不同的版本。這封信是由埃拉託斯提尼給托勒密國王，儘管這封信是偽造的，但作者確實引用了一些真跡埃拉託斯提尼 [1]:-

埃拉託斯提尼向托勒密國王問好。

故事是這樣的：一位古代悲劇性詩人代表米諾斯為格勞卡斯建造了一座陵墓，當米諾斯發現墓穴兩側各有100英尺高時，他說：“你所標出的作為皇家安息之地的墳墓太小了。讓它再大一倍。在不破壞形式的情況下，迅速將墓的兩側翻一番。”這顯然是個錯誤。因為如果邊是兩倍，表面是四倍，體積是八倍。

這個故事講的是希臘神話中的一個插曲，而不是歷史事實。然而，克里特島Knossos最近的發現表明，至少在一定程度上，這些神話故事是以歷史事件為基礎的。神話中，格勞克斯，克里特國王米諾斯和他的妻子帕西帕，在孩提時代就死於一罐蜂蜜中。

正如我們剛才所看到的，使立方體加倍的問題的起源可能有點模糊，但毫無疑問，希臘人早就知道如何解決正方形加倍的問題。對於，取一個正方形的ABCD並在對角DB中繪製。在BD上構造一個正方形BDEF。然後很容易看出BDEF是雙ABCD。使矩形加倍有點困難，但這也是已知的，並由歐幾里得在第二冊中元素顯然是早期工作的一部分。

在使立方體加倍的問題上邁出的第一步是希波克拉底可能在問題首次出現後不久。然而，這一問題似乎已經以更普遍的形式加以審議，即：(i)若要查詢其與給定立方體的比率等於兩條給定行的比率的立方體，請執行以下操作。現在希波克拉底將這一問題減少到以下幾個方面：(二)給定兩行，找出它們之間的兩個平均比例。

即給定線a，ba,b發現x，yx,y使.A：x=x：y=y：Ba:x=x:y=y:b.現在，我們對比率的現代理解很容易看出這一點。(i)和(二)都是等價物。為A^{3}：x^{3}=(a：x)^{3}=(a：x)(x：y)(y：B)=a：ba3:x3=(a:x)3=(a:x)(x:y)(y:b)=a:b.因此，如果給我們一個邊邊的立方體aa並想要構造一個多維資料集B：ab:a乘以體積，我們需要構造邊的立方體。xx.

現在，經常在關於使多維資料集加倍的文章中，用最後一段的論點來證明希波克拉底那(i)和(二)都是等價的；例如，請參見[3]。但正如書中所指出的[8]此型別的引數不可用於希波克拉底因此，人們不僅要考慮他如何證明這種等價性，而且還要考慮他如何證明這種等價性。希波克拉底首先想到的是結果。沒有辦法確切地知道這些問題的答案。然而，有一些線索來自於二維案件的問題。歐幾里得在元素，顯示以下兩個問題是等價的：(三、)找出其與給定平方之比等於兩條給定直線之比的平方。

(四、四)給定兩條線，找出它們之間的一個平均比例，即給定的線a，ba,b發現xx使.A：X=x：Ba:x=x:b.再一次現代論證A^{2}：x^{2}=(a：x)^{2}=(a：x)(x：B)=a：Ba2:x2=(a:x)2=(a:x)(x:b)=a:b顯示出給定的正方形aa那麼，如果我們構造一個方的邊xx，它的面積等於B：ab:a是方方的倍aa. 歐幾里得，在元素第六冊，不僅顯示了(三、)和(四、四)但他展示了(四、四)可以用來解決(三、). 希思還建議在[2]那希波克拉底可能是因為他引用了數論歐幾里得氏元素第八冊：-

在兩個立方體數之間有兩個平均比例數，而立方體與立方體之比是邊與邊之比的三份。

然而，熟練的文字分析阿基米德' 關於球體和圓柱體領導作者[8]來推斷出化合物的比率，雖然這是眾所周知的阿基米德，屬於更現代的數學。希波克拉底。不管是什麼理由希波克拉底為了證明將立方體加倍的問題減少到(二)值得注意的是，後來所有數學家都對這個問題進行了討論。(二)而不是原來的配方。

接下來，我們將考慮以下建議的解決方案：阿基塔斯。這是一個相當漂亮的解決方案，顯示出相當突出的創新阿基塔斯. 希思寫字[2]:-

解決辦法阿基塔斯是最了不起的，尤其是當他的約會物件被認為(公元前4世紀上半葉)，因為它不是平面結構，而是三維的大膽構造，確定某一點為三個旋轉曲面的交點.

我們將指明所使用的建築。阿基塔斯由尤託修斯。我們將嘗試對這一結構進行現代解釋，以使其更易於理解，但我們將強調，部分描述中的協調風格絕不存在於阿基塔斯.

圖

考慮在XYxy-直徑平面骨關節炎OA在xx-軸線，其中OO是起源和AA重點(a，0)(a,0)。放任BB是圓圈上的點OB=bOB=b。目的是在aa和bb。延展OBOB與圓周相切AA在這一點上CC。假設我們認為這個數字3-維空間zz-軸在OO直接從圖的平面上出來。現在我們想象一下希思在上面的引文中。一個曲面是圓上的半圓柱體。奧巴OBA從圖的平面上出來。第二種是由總幹事OC當三角形OCAOCA繞線旋轉骨關節炎OA。第三個曲面是透過考慮XZxz-飛機骨關節炎OA因為它的直徑位於XYxy-平面，然後旋轉這個半圓骨關節炎OA哪裡骨關節炎OA在XYxy-飛機OO。這個表面是環面的一半，環面中心的洞只是點。OO.

假設旋轉的三個表面在點處相交。PP。然後PP，躺在半圓柱體上，就在一個點上。NN在圓圈上奧巴OBA。構造的兩個平均比例阿基塔斯然後OPOP和在……上面ON。我們將在一段時間內使用一些座標幾何學來觀察阿基塔斯是正確的，但首先讓我們用尤託修斯，不變，除了我更改的點的名稱，以適應我們的圖表的表示法和上面所描述的。(例如見[7]):-

這是.的解決方案阿基塔斯，由尤德摩斯:

讓這兩條給定的行為OA[=a]它需要在a和b之間構造兩個平均比例。畫出以OA為直徑的圓形OBA，其中OA較大。[OA=a>b]和題詞OB，長度b，並生產它在C，切線在A.想象一個半圓的半圓垂直上升的OBA，而在OA是一個垂直的半圓站在[底座]半圓柱形的。當這個半圓從A移動到B時，直徑的極值O仍然固定，它會切割圓柱形表面，使其運動，並在上面畫出一條粗大的曲線。然後，如果OA保持固定，如果OCA圍繞OA旋轉，與半圓的運動相反，它將透過OC線產生一個圓錐曲面，在其運動過程中，它將滿足在特定點在圓柱體上繪製的曲線。[P]. ...

要用現代數學來看，為什麼要這樣做呢？我們注意到圓柱面有方程。(1) X^{2}+y^{2}=AXx2+y2=ax,圓周面有方程(2) X^{2}+y^{2}+z^{2}=a√(x^2}+y^{2})x2+y2+z2=a√(x2+y2)圓錐面有方程(3) X^{2}+y^{2}+z^{2}=a^{2}x^2}/b^2}x2+y2+z2=a2x2/b2.如果(p，q，r)(p,q,r)是這三個曲面相交的點。OP=√(p^{2}+q^{2}+r^{2})OP=√(p2+q2+r2)當On=√(p^{2}+q^{2})ON=√(p2+q2).現在從(1)和(3) P^{2}+q^{2}+r^{2}=(p^2}+q^{2}){2}/b^{2}p2+q2+r2=(p2+q2)2/b2.

因此A/√(p^{2}+q^{2}+r^{2})=√(p^{2}+q^{2}+r^{2})/√(p^{2}+q^2})=√(p^2}+q^2})/ba/√(p2+q2+r2)=√(p2+q2+r2)/√(p2+q2)=√(p2+q2)/b視需要而定。

透過他的作品尤託修斯，我們知道尤多克斯並給出了立方體加倍問題的解決方案。然而，他的解決方案失敗了，因為尤託修斯在他面前是相當微不足道的錯誤，因此他沒有複製它。沒人相信尤多克斯他的解有一個基本錯誤(他是個非常優秀的數學家。)因此，當他的解決方案被不正確理解的人複製時，錯誤一定是引入的錯誤。保羅·坦納利建議尤多克斯的解決方案是由阿基塔斯我們剛才描述的，實際上是透過投影得到的解阿基塔斯在飛機上建造。但是，希思 [2]暗示尤多克斯曾：-

...作為一位極具獨創性的數學家，他不會滿足於僅僅適應阿基塔斯解的方法。

I [EFR]同意以下評估希思，所以現在我們不太可能知道尤多克斯解決了立方體的翻倍問題。

梅納克姆斯(Menaechmus)據說他在試圖解決將立方體加倍的問題時發現了圓錐曲線。梅納克姆斯(Menaechmus)求兩個平均比例的解由尤託修斯在他對阿基米德' 關於球體和圓柱體.

假設我們被給予a，ba,b我們想找出兩個平均比例x，yx,y它們之間，即A：x=x：y=y：Ba:x=x:y=y:b。使用現代數學，當然這是不可能的梅納克姆斯(Menaechmus)，我們可以看到，在解決問題時，圓錐曲線是如何產生的。現在A/x=y/ba/x=y/b所以XY=abxy=ab,

X/y=y/bx/y=y/b所以Y^{2}=bxy2=bx，和

A/x=x/ya/x=x/y所以X^{2}=ayx2=ay.梅納克姆斯(Menaechmus)給出了兩個解決方案。第一種是矩形雙曲線和拋物線，這是我們列表中的前兩個方程。我們現在看到xx和yy都是從拋物線的交集處找到的。Y^{2}=bxy2=bx和矩形雙曲線XY=abxy=ab。當然，我們必須再次強調，這絕不意味著梅納克姆斯(Menaechmus)解決了這一問題，但從現代的角度看，拋物線和雙曲線是如何進入問題的解決的。他的第二個解決方案梅納克姆斯(Menaechmus)使用兩個拋物線的交集。Y^{2}=bxy2=bx和X^{2}=ayx2=ay這是我們列表中的第二和第三個方程。

關於雙倍立方體問題的最大難題之一是，有一種機械解稱為柏拉圖的機器。現在看來不太可能柏拉圖會給出一個機械的解決方案，特別是考慮到他對這些解決方案的看法。普盧塔克(例如見[7]):-

柏拉圖責備門徒尤多克斯, 阿基塔斯和梅納克姆斯(Menaechmus)為了採用力學和工具手段來解決體積重複的問題；因為他們希望以某種方式找到兩種平均比例，因此他們採用了一種不合理的方法。在這樣的過程中，一個人並沒有失去幾何學中不可挽回的最好的東西，而是透過迴歸到感官的水平，這阻止了一個人創造甚至感知到永恆和無形的形象，其中上帝是永恆的上帝。

有兩種理論柏拉圖解決立方體問題加倍的機器。一種理論是柏拉圖發明了機械的解決方案，以表明設計這樣的解決方案是多麼容易，但更廣泛的理論是：柏拉圖他的機器是他的一個追隨者發明的書院.

埃拉託斯提尼在這個故事中是很重要的，因為問題的歷史是透過他傳達的，也是因為他自己對這個問題的貢獻。他在亞歷山大立了一根柱子，獻給托勒密國王，上面刻著一句警句，是關於他自己解決立方體加倍問題的機械方法的。[2]:-

好朋友，如果你想從任何一個小立方體中得到一個立方體的二倍，並適當地將任何實體轉變成另一個立方體，這是你的力量所在，你可以用這種方法找到一個褶皺、一個坑或一口空井的大盆的尺度，也就是說，如果你這樣在兩個統治者之間抓住了兩個手段，它們的兩端匯合在一起。你不想做困難的事嗎？阿基塔斯“圓柱體”，或切割美拿克摩斯三位一體的圓錐體，或指南針的弧形線條，這是敬神者所描述的。尤多克斯。不，在這些藥片上，你很容易就能找到無數的方法，從一個小的基礎開始。托勒密，你真高興，因為作為一位父親，作為一位年輕的父親，你已經把繆斯和國王所珍視的一切都給了他，而且將來也是如此，天之之神宙斯，也在你的手中得到了權杖。但願如此，讓看見這祭物的人說：“這是我的恩賜。埃拉託斯提尼“古蘭經”。

那是什麼機器埃拉託斯提尼為了解決問題而發明的？它由兩條平行線組成，它們之間有三角形，如上圖所示。這裡聲發射AE和生署DH是需要找到兩個平均比例的兩個長度。現在保留第一個三角形AMFAMF修正了，但是允許三角形MNGMNG和NQHNQH在框架內滑動斧頭AX和安永EY。旋轉斧頭AX直到它透過DD但是在這樣做的時候要確保BB和CC在這條旋轉線切割的地方MFMF和吳NG繼續躺在一邊鎂MG和氨NH在向左移動的兩個三角形中，允許此配置保持為可能。三角形向左滑動，直到到達兩個圖的底部。在這最後的圖表中高爐BF和CGCG之間的兩個平均比例聲發射AE和生署DH.

現在埃拉託斯提尼在上面引用的評論中，他的機器能夠找到兩個以上的平均比例。如果一個人需要“無數的平均”比例，那麼你就需要把這個數目的可移動三角形放入他的機器中，同樣的程式也會找到“無數”的平均比例。

解決這個問題的其他辦法是菲倫和蒼鷺都給出了相似的方法。它們的解由圓與矩形雙曲線的交點有效地產生。尼可米德斯，他對埃拉託斯提尼力學解，給出了一種構造方法，該構造採用了他也用來解決三角剖分問題的Conchoid曲線。施工詳情見[2]. 迪克勒斯還發明瞭一種特殊的曲線來解決立方體加倍的問題，即順式曲線。

雖然發明了許多不同的方法來使立方體翻一番，而且在嘗試中也有了顯著的數學發現，但古希臘人永遠也找不到他們真正想要的解決辦法，那就是用尺子和指南針構造的方法。他們永遠找不到這樣的建築，因為這樣的建築是不可能建成的。然而，古希臘人不可能證明這一結果，因為它要求數學遠遠超過他們所發展的任何東西。然而，可以公平地說，儘管他們無法證明統治者和指南針的構造是不可能的，但古希臘數學家中最好的人直覺地知道，這的確是不可能的。

不可能的證明必須等待數學的證明。19TH世紀。辯論的最後部分是由皮埃爾·萬澤爾。在……裡面1837 萬澤爾發表的證據劉維爾氏日刊的：-

...確定一個幾何問題是否可以用標尺和圓規解決的方法。

高斯他曾說過，用尺和羅盤不能解決立方體倍和角的問題，但他沒有給出任何證明。在這裡1837紙萬澤爾是第一個證明這些結果的人。改進的證明後來由查爾斯·斯特姆但他沒有出版。