三角形全等性質,怎麼證明三角形全等?是初中數學裡的一個基礎常用知識點,重點,也是一個難點。在後面的幾何學習中,經常需要用到三角形全等的知識來解決問題。所以,熟練掌握三角形全等的性質和判定定理,顯得尤為重要
直接根據條件和圖形,可以證明兩個三角形全等的題型,估計大多數同學都能做出來。但是有些題目和圖形,需要新增輔助線,很多同學就顯得有些艱難。
今天小編,就整理了6道新增輔助線證明三角形全等的基礎題型。這6道題,題目不難,但是包括了幾種常用的新增輔助線的型別和方法,同學們舉一反三,多思考多總結。
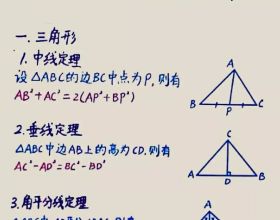
第1題,連線AC和AD,構造兩個全等三角形,對應邊相等得到一個等腰三角形。根據等腰三角形的三線合一的性質,證明出結論。
第2題,等腰直角三角形,斜邊上的中點,一般連線斜邊的中線,得到三條邊相等,得幾個45°角相等。這是這一類題型的輔助線新增的方法。
第3題,這個輔助線的作法和倍長法有點類似,但若只是倍長,就找不到角相等。那麼做平行線,就有內錯角相等,再根據題意的其他條件,得出兩個三角形全等。
第4題,要求證明BD平分∠ABC,第一想到的是角平分線的性質的逆定理。過點D做角兩邊的垂線,構造兩個三角形全等,得到點到角兩邊的距離相等。
如果這道題,方老師要求大家換一個思路新增輔助線,同學們認真思考一下,看要怎麼證明?比如在NC上擷取NE=BM。
第5題,這類證明一條線段等於幾條線段之和的題型,就是想辦法新增輔助線,進行相等的線段進行代換,把幾條線段放到一條線段上。那麼線段相等,一般就是需要構造三角形全等。
第6題,就是我們最常見的倍長中線法,構造三角形全等。這個倍長中線的輔助線新增方法,在很多的題型中,都用得到。
新增輔助線是解決數學幾何問題的基本方法,同學們從簡單的題型練起,一定要勤于思考,善於總結,得出常用的解決問題的方法。這樣,初中數學基礎才會紮實,考試成績才不會差。