編輯 | 蘿蔔皮
追求不具有傳統可測量物體特性的分餾粒子,例如真空中的裸粒子(如電子)和基本激發(如磁振子),是物理學中的一項挑戰。
在某些磁鐵中,粒子自旋——視覺化為粒子圍繞其旋轉的軸——都被迫對齊,而在其他磁鐵中,它們必須改變方向。但在少數材料中,這些對齊或反對齊的趨勢相互競爭,導致所謂的失磁。這種情況意味著自旋在方向之間波動,即使在人們期望穩定的絕對零溫度下也是如此。這會產生一種奇異的物質狀態,稱為量子自旋液體。
「這種有趣且不同尋常的量子自旋『液態』狀態有望具有與普通『固態』系統不同的獨特量子糾纏特性。」 日本理化學研究所(RIKEN)的 Yusuke Nomura 解釋說,「而且這些糾纏特性可能對量子計算機中的量子計算有用。」
日本理化學研究所、豐田理化研究所和早稻田大學的研究人員合作,展示了一種用於量子多體系統的機器學習方法,該方法可以預測量子材料的複雜和奇異狀態的特性。這一進步可能促進未來量子計算機的發展。
該研究以「Dirac-Type Nodal Spin Liquid Revealed by Refined Quantum Many-Body Solver Using Neural-Network Wave Function, Correlation Ratio, and Level Spectroscopy」為題,於 2021 年 8 月 12 日釋出在《PHYSICAL REVIEW X》。
簡介
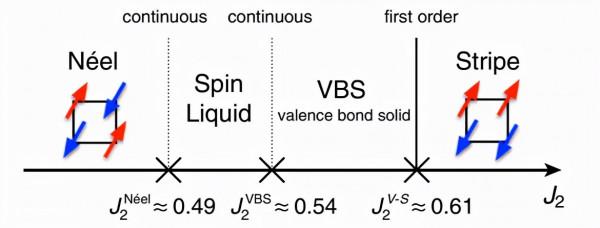
該方法已經達到了最先進的精度,在自旋 1/2 受挫海森堡模型中,令人信服地揭示了 0.49≲J2/J1≲0.54 區域中量子自旋液體(QSL)相的存在,其中最近鄰和次最近鄰交換分別為 J1 和 J2。這是透過結合稱為相關比和水平光譜方法的尖端計算方案,來減輕有限尺寸效應,從而實現的。
圖示:透過 RBM + PP 方法獲得的方格 J1-J2 海森堡模型 (J1 ¼ 1) 的基態相圖。(來源:論文)
基態相關性與當前分析中發現的激發光譜之間的定量一一對應關係能夠可靠地識別和估計 QSL 及其性質。包含單線態和三線態無間隙狄拉克色散的自旋激發光譜表明,在獨特的 QSL 相中出現了無間隙分級自旋 1/2 狄拉克型自旋子。
揭示了與 Néel 反鐵磁和二聚體相關性的共存和雙冪律衰減的未探索的臨界行為。兩個相關的冪律衰減指數在 QSL 階段隨 J2/J1 不同而不同,因此除了滿足兩個相關的對稱性的單個點外,具有不同的值。這裡揭示的銅酸鹽 d 波超導體激發的同構性,暗示了當前 QSL 和超導性之間的緊密聯絡。這一成就表明,使用機器學習技術的量子狀態表示(主要限於基準測試)是研究量子多體物理學中的重大挑戰的有前途的工具。
具體做了什麼
研究人員使用高度準確的機器學習方法 RBM + PP 研究了 2D J1-J2 海森堡模型。該研究的成就主要為以下幾點:相圖的定量估計,對 QSL 性質的有用見解以瞭解其性質,以及在基態和激發結構之間建立一對一的對應關係。
圖示:(a) 自旋-自旋和 (b) 二聚體-二聚體相關性的相關比的系統大小依賴性,它們分別用於檢測 Neel-AFM 和 VBS 的相界。(來源:論文)
首先,透過將 RBM + PP 與相關比和水平光譜法相結合,研究人員已經能夠透過兩個獨立的分析可靠地外推到熱力學極限。兩者在前所未有的水平上達成的協議為有限 QSL 區域 0.49 ≲ J2/J1 ≲ 0.54 提供了確鑿的證據。
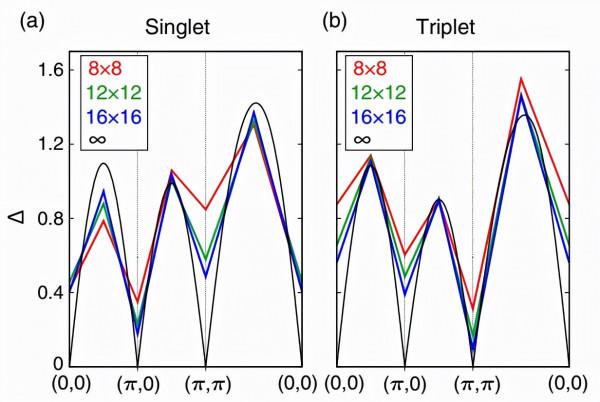
圖示:QSL相的低激發。(來源:論文)
QSL 的特徵是反鐵磁(與 Néel 順序相關)和二聚體(與 VBS 順序相關)相關的代數和共存相關性的雙重性質,之前由於對稱性差異,它們被認為是不相容的。所闡明的雙重性質在激發性質中也得到了一致的體現:研究人員已經在單重態和三重態激發區(分別與二聚體-二聚體和自旋-自旋關聯相關)確定了具有無間隙點(0,0)、(π,0)、(0,π)和(π,π)的狄拉克型色散。激發結構與具有無間隙狄拉克色散的分級自旋 1/2 自旋子的出現一致。有趣的是,這兩個相關性的冪律衰減指數作為 J2/J1 的函式而變化,除了 J2=0.52 附近的單個點外不重合,這對 QSL 的規範結構施加了實質性約束。
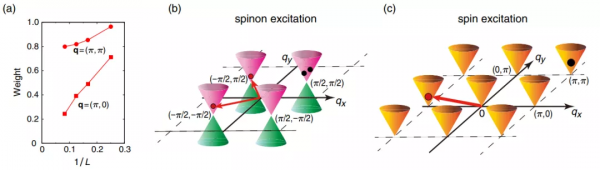
圖示:無間隙點周圍的似是而非的自旋子色散示意圖。(來源:論文)
最後,綜合計算揭示了 J1-J2 海森堡模型中基態和激發態結構之間的基本「對應定律」。透過建立相圖,研究人員證明基態的演變確實對映到由水平交叉引起的激發結構的變化,以指紋方式一一對應。同時表明,在 QSL 相(基態特性)的真實空間中,二聚體-二聚體和自旋-自旋相關函式的共存冪律衰減分別一致地證實了單線態和三線態激發的無間隙結構。這種一一對應在物理學中具有基礎意義,因為漲落耗散定理和久保公式中平衡和非平衡激發態之間的一一對應為理解線性響應奠定了基礎。
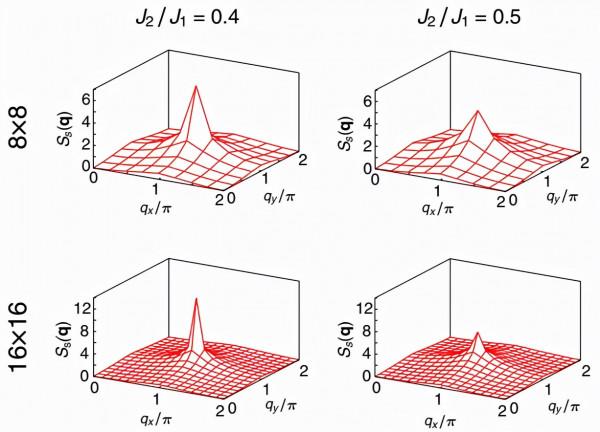
圖示:自旋-自旋相關性的結構因子 Ss(q)。(來源:論文)
RBM 波函式與 PP 狀態和量子數投影相結合,能夠對 QSL 進行如此準確、系統和全面的闡明,並深入瞭解無間隙相關性的二元性和對應定律 - 易處理的計算成本內的藝術精度:RBM + PP 方法 [O(N3site)] 的高精度和易處理的計算成本縮放,對於為大型系統準備全面的高質量資料是必要的。
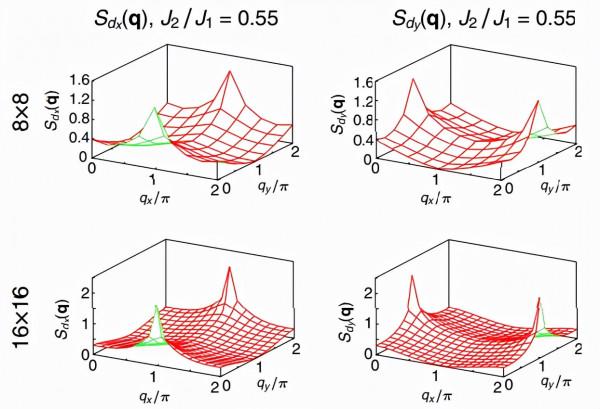
圖示:二聚體-二聚體相關性 Sdx(q)和 Sdy(q) 的結構因子。(來源:論文)
結語
到目前為止,機器學習方法主要應用於已知解決方案的基準問題。透過將 RBM+PP 波函式與前沿方法相結合以減少有限尺寸校正,研究人員成功地在長期存在的挑戰性問題中發現了 QSL。這一成就開闢了一條適用於應對量子多體系統巨大挑戰的數值方法的新途徑。
該研究為在真實材料中實現量子自旋液相提供了有用的指導。但有一個更廣泛的資訊:該研究強調了機器學習作為解決物理學重大挑戰的工具的力量。「使用機器學習作為一種新穎的工具,我們解決了物理學中一個長期存在的問題,這個問題在無人幫助的情況下很難解決。」Nomura 說,「未來,除了人腦之外,『機器大腦』的使用將為其他尚未解決的問題提供新的線索。這標誌著物理學研究新時代的開始。」
論文連結:https://journals.aps.org/prx/abstract/10.1103/PhysRevX.11.031034
相關報道:https://phys.org/news/2021-11-quantum-liquids-machine.html