洛倫茲力作用下圓周運動的圓心的確定

對於求解洛倫茲力作用下的圓周運動的相關問題，圓心的確定是解題的關鍵，圓心的確定主要依據以下3點。

①.兩速度垂線的交點

速度的垂線即為洛倫茲力所在直線，也就是半徑所在直線，兩條不在同一條直線上的半徑交點就是圓心，洛倫茲力方向永遠指向圓心。分別從入射點和出射點引出兩速度的垂線。

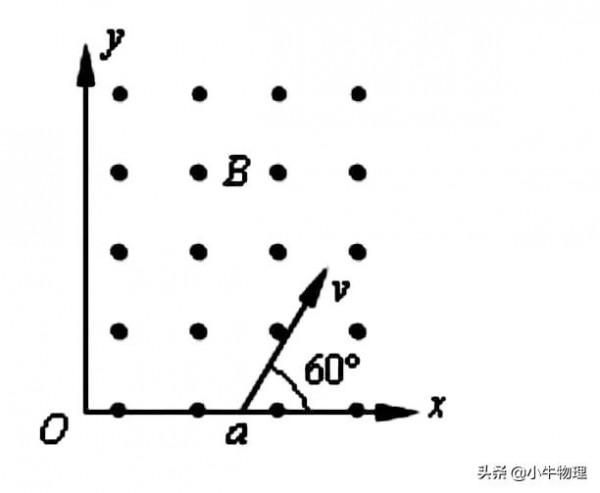
例題：如圖所示，一個質量為m、電荷量為q的帶電粒子從x軸上的P（a，0）點以速度v，沿與x軸正方向成60°的方向射入第一象限內的勻強磁場中，並恰好垂直於y軸射出第一象限。求勻強磁場的磁感應強度B和射出點的座標。

【解析】垂直y軸射出，圓心一定在y軸上，從入射點a點作速度的垂線，與y軸交點必定為圓心。再由幾何關係計算半徑。

②.兩弦中垂線的交點

在軌跡圓中，把入射點和出射點連線起來必定為弦，根據幾何知識，圓心一定在弦的中垂線上。

③.兩速度夾角補角的角平分線

把速度線延長交於一點，從該點作出速度夾角補角的角平分線，圓心必定在角平分線上。

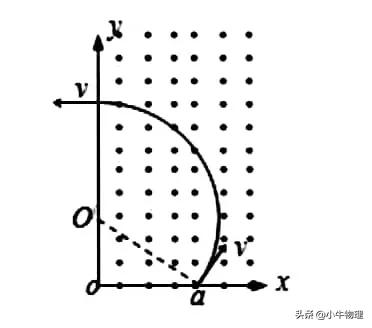
例題：一質量為m，帶電荷量為q的粒子，以速度v₀從O點沿y軸正方向射入磁感應強度為B的一圓形勻強磁場區域，磁場方向垂直於紙面，粒子飛出磁場區域後，從b處穿過x軸，速度方向與x軸正方向夾角為30°，如圖所示，不計粒子重力，求：

（1）圓形磁場區域的最小面積；

（2）粒子從O進入磁場區域到達b點所經歷的時間及b點的座標。

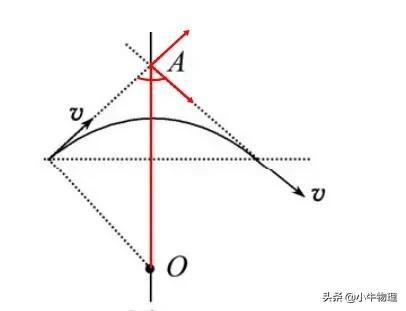
【解析】軌跡圓的圓心必定在兩速度夾角補角的角平分線上的一系列圓上。

根據題意，O點已經進入磁場，圓心也一定在速度垂線上，結合起來分析，原因在角平分線和垂線的交點上，如圖所示，

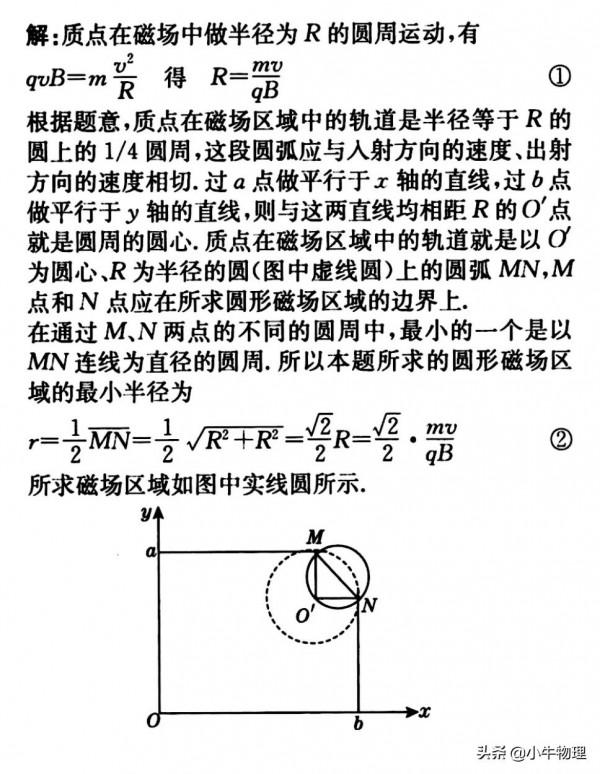
例題：一帶電質點，質量為m，電量為q，以平行於Ox軸的速度v從y軸上的a點射入圖中第一象限所示的區域。為了使該質點能從x軸上的b點以垂直於Ox軸的速度v射出，可在適當的地方加一個垂直於xy平面、磁感應強度為B的勻強磁場.若此磁場僅分佈在一個圓形區域內，試求這圓形磁場區域的最小半徑.重力忽略不計.

【解析】圓心在速度夾角補角的角平分線上，而半徑已經確定，軌跡圓是確定的。

確定圓心的方法也可以這樣總結為：

⒈半徑法

⒉角平分線法

⒊中垂線法

⒋綜合法

在實際應用中，往往是幾種方法結合使用，謂之為綜合法.