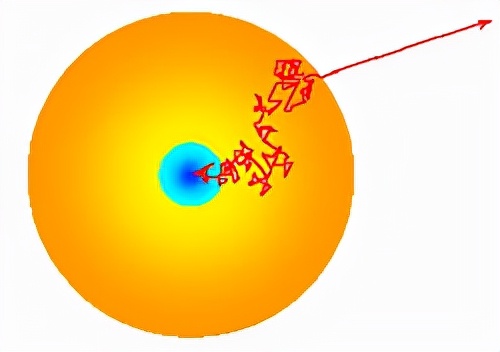
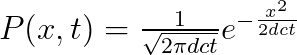有一個流行的說法:光子從太陽核心到太陽表面需要數萬年的時間,但從太陽表面到地球只需要8分鐘。在這個說法背後,是光子在太陽內部的布朗運動,在數學上我們可以用隨機遊走模型進行計算。
核聚變產生的光子會被其它原子重新吸收並釋放到另一個方向,在這期間它平均移動了一個距離d;給定d和光速c,我們可以計算出平均時間步長和空間步長;太陽的尺寸可以用步長進行衡量,最後,光子到達太陽表面的平均時間就能被計算出來。
開始數學計算
如果一個粒子平均每Δt時間內以隨機方向(左右各50/50)移動一個Δx的距離,那麼該粒子在特定時間特定地點的機率P(x,t)滿足下列方程:
接下來,我們在等式的兩邊減去P(x,,t-Δt),並巧妙構造出微分方程。
在太陽這個例子中,平均自由程Δx=d,這意味著在光速下,Δt = d/c,代入上面的微分方程,
我們可以解得:
我們關心的是時間,我們要計算的是在某個時間T,粒子超出太陽半徑R的機率,因此我們可以dx進行積分。由於對稱性,只需要關心一邊的情況就夠了,因此x的範圍從R到正無窮,並且式子還要乘以2,得到:
對於這麼複雜的方程,我們可以用高斯誤差函式進行重新表達:
之所以這麼做,是因為數學太難了,前人有研究結果我們就直接套用,可以省下很多計算時間。
現在,我們可以得到,當erf()=1/2時,光子有50%的機率已經逃脫了太陽,此時:
代入R=7×10^8米,c=3×10^8米/秒,d=0.0001米,我們可以解得T=110萬年。
當然,太陽的不同部分有不同的d值,這使得嚴謹的計算變得更加困難。考慮到我們對太陽的瞭解,有些人認為真實時間應該在10萬年左右。此外,我們的計算也忽略了很多事實,比如把太陽當成一個線段而不是球體,還有光子被吸收和釋放的時間等。因此,這更像是一種假設計算。