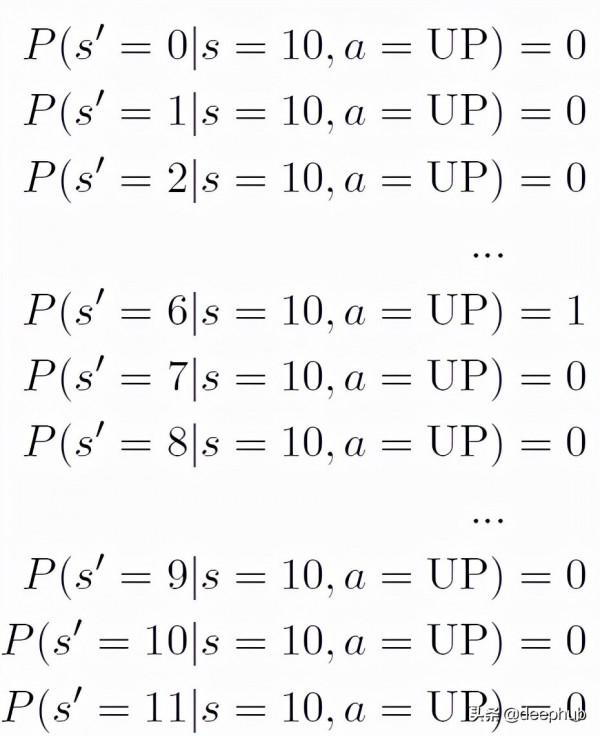馬爾科夫決策過程基本概念

馬爾可夫決策過程(Markov decision process, MDP)是人工智慧中的一個重要概念，也是強化學習的理論基礎之一。在今天的文章中，我們使用來自Stuart Russell和Peter Norvig的《Artificial Intelligence: A Modern Approach》一書中的網格例子來介紹MDP的基本概念。

我們的吃豆人遊戲

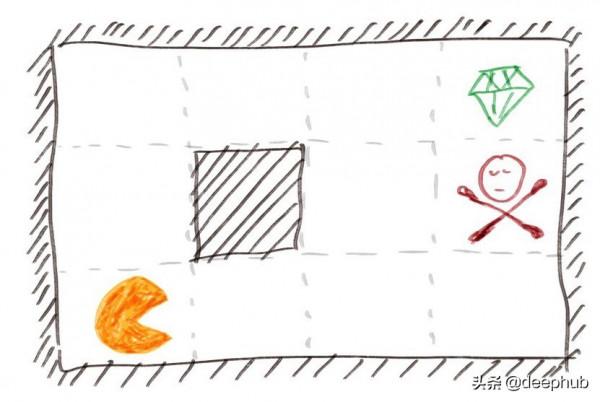
這裡我們有一個 4×3 的網格世界，有一個機器人從左下角開始並在這個 2D 世界中移動來玩遊戲。

世界示例

我們的機器人可以向四個方向移動：上、下、左、右，與吃豆人的相似之處是我們的世界被不可通行的牆包圍。黑色方塊代表的邊界內也有不可透過的牆。

右上角正方形中的綠色菱形代表終點線。如果我們到達這個方格，我們就會贏得這場比賽並獲得很多積分（在本例中為 +1）。

在吃豆人中，總有鬼魂試圖傷害你。在我們的遊戲中，我們有一個帶有紅色毒藥的方塊。如果我們進入這個方格，我們就會輸掉比賽並受到很多懲罰（在這個例子中是 -1）。

所有其他白色方塊都是正常的方塊。每次我們進入其中一個時，我們都會失去少量點數（在本例中為 -0.04）。如果我們隨機移動，希望最終幸運地到達綠色菱形，那麼我們每走一步就會損失 0.04 分，從而損失很多分。這就相當於機器人的電力系統，每走一步需要消耗一定的電量，所以機器人每走一步就要減去點積分，以保證最低的消耗。

為簡單起見，我們假設我們的機器人總是從左下角開始，如上圖所示。

綜上所述，在玩這個遊戲的時候，我們希望儘可能快地獲得+1點，而一路上付出最少的-0.04，並且我們絕對要避免在紅毒中以-1結束遊戲。

MDP的定義

在《Artificial Intelligence: A Modern Approach》中，MDP 被定義為

具有馬爾可夫轉移模型和附加獎勵的完全可觀察的隨機環境的順序決策問題稱為馬爾可夫決策過程或 MDP，由一組狀態（具有初始狀態 s₀）組成；每個狀態下的一組動作；一個轉換模型 P(s'| s, a);和獎勵函式 R(s)。

讓我們用我們的例子來分解這個定義中的一些關鍵字。

代理（又叫智慧體）是指機器人或吃豆人或我們放置在這個世界中的任何東西，它會環顧四周尋找可能的移動，考慮可能移動的利弊，做出下一步移動的決定，並執行移動。

環境是指世界的樣子和世界的規則。在我們的例子中，環境包括我們的世界有多大，牆在哪裡，如果我們撞到牆會發生什麼，鑽石在哪裡，如果我們到達那裡，我們得到多少分，毒藥在哪裡，如果我們到達還有我們輸了多少分，等等。

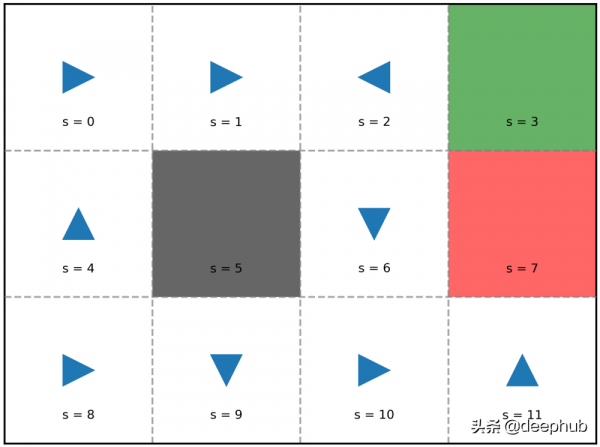
MDP 中的狀態是指我們代理的狀態，而不是我們環境的狀態。在 MDP 中，環境是給定的並且不會改變。相比之下，我們的代理可以將狀態從先前的移動更改為當前的移動。在這個示例中代理有 12 個狀態，代表我們的代理可能處於的 12 個方格。從技術上講，我們的代理不能處於黑色方格中，但為簡單起見，我們仍將黑色方格視為一個狀態。在 MDP 中，我們使用 s 來表示狀態，在我們的示例中，我們稱它們為 s = 0, 1, 2, ..., 11。

動作是指我們的代理在每個狀態下可以採取的動作。每個狀態的一組可能的操作不一定相同。在我們的示例中，對於每個狀態 s，我們有四個可能的動作 A(s) = {up, down, left, and right}。我們使用 a 來表示動作。

獎勵是指我們進入一個狀態時獲得的積分。在我們的示例中，對於不同的狀態，它是 +1、-1 或 -0.04。獎勵僅依賴於狀態，這個從狀態到獎勵的函式表示為 R(s)。無論我們之前的狀態如何，我們在進入某個狀態時都會獲得相同的獎勵。例如，當 s = 3 時，r = R(s) = R(3)= +1。無論我們從左邊的方格向右移動到它，還是從它下面的方格向上移動到它，我們都會得到相同的 +1 獎勵。

累加獎勵意味著來自不同動作的獎勵是累積的。在我們的示例中，我們的最終積分（總獎勵）是從鑽石或毒藥獲得的積分與沿途可透過的方塊獲得的積分相加。不僅是最後一格獲得的獎勵，一路上獲得的所有小獎勵也很重要。在 MDP 中，我們假設我們可以將這些獎勵加在一起。

轉換模型告訴我們，如果我們在某個狀態下選擇某個動作，我們將進入下一個狀態。這通常表示為表 P。如果我們處於狀態 s 並且我們選擇一個動作 a，那麼 s' 成為下一個狀態的機率是 P(s'| s, a)。

如果我們假設我們的世界是確定性的，那麼我們預期的移動方向總是會實現。例如，如果我們在 s = 10 並且我們選擇 a = UP，我們肯定會進入一個新的狀態 s' = 6。

這可以被表示為：

作為機率分佈，所有 12 個 s' 的 P(s'| s = 10, a = UP) 之和總是等於 1。

隨機意味著我們的世界不是我們上面假設的確定性的。從某個狀態開始，如果我們選擇相同的動作，我們不能保證進入相同的下一個狀態。在我們的這個遊戲中，可以將其視為我們的機器人以某種方式出現故障的可能性。例如，如果它決定向左走，那麼實際上向左走的可能性很大。然而，它有一個很小的可能性，無論它有多小，它都會瘋狂地向左以外的方向移動。

按照書中的例子，實際朝預期方向移動的機率是 0.8。向預定方向左移 90 度的機率為 0.1，向預定方向向右移動 90 度的機率為 0.1。

例如，如果我們在 s = 10 並且我們選擇 a = UP，我們有 0.8 的機率進入預期的新狀態 s' = 6。我們也有 0.1 的機率到達 s' = 9 並且到達 s' = 11 的機率為 0.1。

這可以寫成下面這樣：

這是當 s = 10 且 a = UP 時的轉換模型。現在對於每對狀態 s 和動作 a，我們可以像這樣寫出到達每個新狀態的機率。將所有這些組合在一起，我們得到了轉換模型 P。我們有 12 種可能的狀態和 4 種可能的動作。因此，我們的過渡模型 P 的維度為 12×4×12，共有 576 個機率值。

完全可觀察意味著我們的代理是知道世界的全部樣子以及它自己目前在那個世界中的位置。從某種意義上說，我們可以說我們的代理有上帝視角。它可以訪問在每次移動中找到最佳決策所需的所有知識。這裡的知識指的是我們的獎勵函式 R(s) 和過渡模型 P(s'| s, a)。

順序意味著我們當前的情況受先前決定的影響。出於同樣的原因，所有未來的情況都會受到我們當前決定的影響。例如，如果我們從 s = 8 開始並決定向上移動作為我們的第一步，那麼我們到達 s = 4。我們無法在下一步移動中到達 s = 10。如果我們選擇向右移動作為我們從 s = 8 開始的第一步，那麼我們到達 s = 9。現在我們可以透過向右移動到達 s = 10。換句話說，我們能否在第二步中達到 s = 10 取決於我們在第一步中的選擇。

馬爾可夫意味著我們的世界是沒有記憶的。這似乎與我們對順序的定義相反，但實際上它們具有完全不同的含義。順序意味著我們能否在第二步中達到 s = 10 取決於我們在第一步中所做的選擇。

但是無記憶是什麼意思？

這意味著無論我們如何到達狀態 s = 10，無論我們是從 s = 9 或 s = 11 或 s = 6 到達它，一旦我們處於該狀態，我們總是面臨相同的情況，具有相同可能的行動的集合。如果我們做出決定，將會發生什麼並不取決於過去發生了什麼。換句話說，這只是意味著無論你在遊戲中做了什麼，P(s'| s, a) 在整個遊戲過程中都不會改變。

當我們第 100 次達到 s = 10 時，我們將面臨與第一次達到相同的動作選擇。如果我們在這個狀態下選擇某個動作，結果總是遵循相同的機率分佈。如果某個動作是我們第一次到達該狀態時狀態 s = 10 的最優動作，那麼該動作始終是該狀態的最優動作。

網格世界的程式碼實現

我們使用 csv 檔案來表示我們的世界地圖，其中 0 為可透過的白色方塊，1 為綠色方塊，2 為紅色方塊，3 為黑色方塊。對於我們的示例，csv 檔案如下所示：

0,0,0,1
0,3,0,2
0,0,0,0

我們使用以下程式碼來實現網格世界示例。每種型別方塊的獎勵由字典獎勵表示。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
class GridWorld:
def __init__(self, filename, reward=None):
if reward is None:
reward = {0: -0.04, 1: 1.0, 2: -1.0, 3: np.NaN}
file = open(filename)
self.map = np.array(
[list(map(float, s.strip().split(","))) for s in file.readlines()]
)
self.num_rows = self.map.shape[0]
self.num_cols = self.map.shape[1]
self.num_states = self.num_rows * self.num_cols
self.num_actions = 4
self.reward = reward
self.reward_function = self.get_reward_table()
self.transition_model = self.get_transition_model()
def get_state_from_pos(self, pos):
return pos[0] * self.num_cols + pos[1]
def get_pos_from_state(self, state):
return state // self.num_cols, state % self.num_cols

獎勵函式

正如我們上面解釋的，獎勵函式 R(s) 僅依賴於狀態 s。我們使用以下程式碼為每個 s 生成獎勵函式 R(s) 的結果。

class GridWorld:
def get_reward_function(self):
reward_table = np.zeros(self.num_states)
for r in range(self.num_rows):
for c in range(self.num_cols):
s = self.get_state_from_pos((r, c))
reward_table[s] = self.reward[self.map[r, c]]
return reward_table

轉換模型

讓我們回顧一下我們的遊戲規則。如果我們撞到一堵牆，我們會被彈回並留在原處。如果我們想向上或向下移動，實際上向上或向下移動的機率為 0.8，向左移動的機率為 0.1，向右移動的機率為 0.1。同樣，如果我們想向左或向右移動，實際上向左或向右移動的機率為 0.8，向上的機率為 0.1，向下的機率為 0.1。

我們使用以下程式碼生成轉換模型。

class GridWorld:
def get_transition_model(self, random_rate=0.2):
transition_model = np.zeros((self.num_states, self.num_actions, self.num_states))
for r in range(self.num_rows):
for c in range(self.num_cols):
s = self.get_state_from_pos((r, c))
neighbor_s = np.zeros(self.num_actions)
for a in range(self.num_actions):
new_r, new_c = r, c
if a == 0:
new_r = max(r - 1, 0)
elif a == 1:
new_c = min(c + 1, self.num_cols - 1)
elif a == 2:
new_r = min(r + 1, self.num_rows - 1)
elif a == 3:
new_c = max(c - 1, 0)
if self.map[new_r, new_c] == 3:
new_r, new_c = r, c
s_prime = self.get_state_from_pos((new_r, new_c))
neighbor_s[a] = s_prime
for a in range(self.num_actions):
transition_model[s, a, int(neighbor_s[a])] += 1 - random_rate
transition_model[s, a, int(neighbor_s[(a + 1) % self.num_actions])] += random_rate / 2.0
transition_model[s, a, int(neighbor_s[(a - 1) % self.num_actions])] += random_rate / 2.0
return transition_model

因為比較小，所以可以直接可視化出來：

讓我們檢查一下我們的模型是否有意義。例如，如果我們看 s = 8，當動作向下時，我們有 0.8 的機率向下然後撞牆並彈回 s' = 8，0.1 的機率向左走然後撞牆並返回 s' = 8，向右走併到達 s' = 9 的機率為 0.1。因此，s' = 8 對應於 p = 0.8 + 0.1 = 0.9，而 s' = 9 對應於 p = 0.1。

策略

策略是指在每個狀態下要採取什麼行動的指令。它通常表示為 π，它是 s 的函式。

例如，如果 s = 2 且 π(s) = π(2) = RIGHT，那麼每當代理處於狀態 s = 2 時都會執行 RIGHT 的動作。它是否真的可以走到右邊的方塊是另一個故事，這取決於轉換模型中的機率。關鍵是，不管結果如何，只要策略返回應該走到哪裡，代理總是認為策略是正確的並且執行。

我們檢視策略的出發點是簡單地生成一個隨機策略並將其視覺化。

class GridWorld:
def generate_random_policy(self):
return np.random.randint(self.num_actions, size=self.num_states)

假設這個隨機過程生成了以下策略。

我們可以明確地寫出這個策略：π(0) = RIGHT, π(1) = RIGHT, π(2) = LEFT, … π(11) = UP。

乍一看，這種隨機生成的策略似乎不起作用。例如，我們從s = 8開始，政策要求向右進入了s = 9，然後政策說向下。然而，s = 9的底部是一堵牆。我們只是撞到那堵牆，然後反彈回s = 9。似乎我們在s = 9處卡住了。

我們不會永遠被困在 s = 9 的原因是我們處於一個隨機的世界。即使策略告訴我們向下並且我們遵循該策略，我們最終在 s = 8 中的機率仍然為 0.1，而在 s = 10 中的機率為 0.1。

策略的執行

現在我們至少有一個策略，儘管它可能看起來不是很好。讓我們看看如果我們執行它會發生什麼。

class GridWorld:
def execute_policy(self, policy, start_pos=(2, 0)):
s = self.get_state_from_pos(start_pos)
total_reward = 0
state_history = [s]
while True:
temp = self.transition_model[s, policy[s]]
s_prime = np.random.choice(self.num_states, p=temp)
state_history.append(s_prime)
r = self.reward_function[s_prime]
total_reward += r
s = s_prime
if r == 1 or r == -1:
break
return total_reward

如果我們當前處於狀態 s，則我們的策略 a = π(s)。由於我們的世界是隨機的，我們使用 numpy.random.choice 根據 P(s'| s, π(s)) 給出的機率分佈來選擇 s'。

因為這個過程是隨機的，不同的執行可能會有不同的結果。讓我們嘗試一下。

這個特定執行的狀態歷史是 [8, 9, 9, 9, 9, 10, 10, 6, 10, 11, 7]。我們從 8 開始，以 0.8 的機率進入 9；然後我們嘗試下降 3 次，然後彈回 9；然後以 0.1 的機率，我們移動到 10，然後是 11，最後不幸的是 7。沿著這條路徑我們使用 10 移動。我們收到的總獎勵是 -0.04 *10 加 -1 等於 -1.4 。

這只是一次執行，我們可能在這一次執行中不走運。讓我們使用蒙特卡羅方法來評估該策略的好壞。對於這個例子，讓我們重複執行 10,000 次並記錄我們在每次執行中獲得的總獎勵。