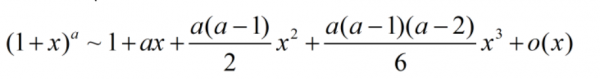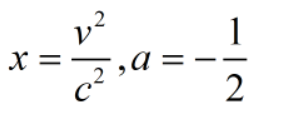提示：本作較為硬核，為了防止讀不懂，您可以先閱讀筆者前日所作：《四維時空的形式》系列科普內容。（文章在筆者主頁可以找到）
今天文章的主角是：質量，能量，哈密頓函式Ψ
奇怪的引力場效應
首先，讓我們繼續講作用量S:它是這個積分關係式。
上式中，S為作用量，c為光速，m為粒子的質量 dt為無限小時間間隔， 積分符號代表了無窮加和的思想。
接著，我們對它求個導，可以得出：
我們發現：
這不正是相對論中能量E的表示式嘛!
根據泰勒公式：我們有這個表示式：
泰勒公式o（x）代表n階無窮小量
將式中的x和a等效替換掉
因為我們日常生活中的速度遠遠地小於光速c，我們可以得到：
這就不是動能公式和質能公式的相加嗎？
上面兩個是我們初中就知道的公式
在專業領域裡，我們常常把m用m0表述，稱它為：靜能，寓意“物體相對靜止時具有的能量”而動能公式1/2mv^2，想必大家已經耳熟能詳了。
扭曲時空：奇妙的引力場
前方核能：只需瞭解即可，無需深入理解原因：
一個靜止物體的能量除了組成其粒子的靜能外，還括粒子的動能和它們的相互作用能。在相對論力學中，質量守恆定律並不一定成立，複合物體的質量並不等於其各部分質量之和（靜止質量和引力質量並不一定相等），只有包含粒子靜能在內的能量守恆定律是成立的。
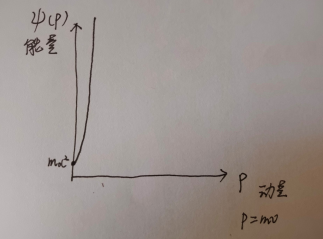
我們想象中的能量的樣子
接著，今天的壓軸嘉賓閃亮登場：他就是能量-動量哈密頓函式：
哈密頓函式
字母Ψ其實就是能量E，為什麼用Ψ呢，因為它長得好看。
也可以寫成這樣子：
動量p是能量Ψ的函式
它的影象大致是：
函式關係圖，mc^2代表靜能
當速度v遠小於光速c時，我們有：
經典體系的哈密頓函式
可以看出，當質量不變時，它只是個一次函式（y=kx+b型）
整理文獻不易，喜歡就請點個關注吧，筆者寫作的極大動力來自諸君的支援
