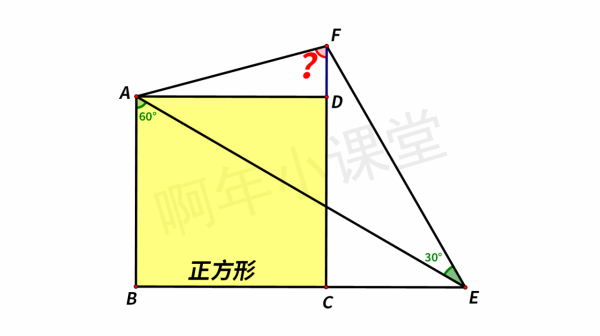
如圖,四邊形ABCD為正方形,∠BAE=60°,∠AEF=30°,求∠AFC的度數。這題怎麼做呢?
四邊形ABCD為正方形,∠BAE=60°,可得∠AEB=30°,
而∠AEF=30°,所以AE為∠BEF的角平分線。
看到角平分線,大家想到了什麼?
角平分線有這樣一個性質,角平分線上的點到角兩邊的距離相等。
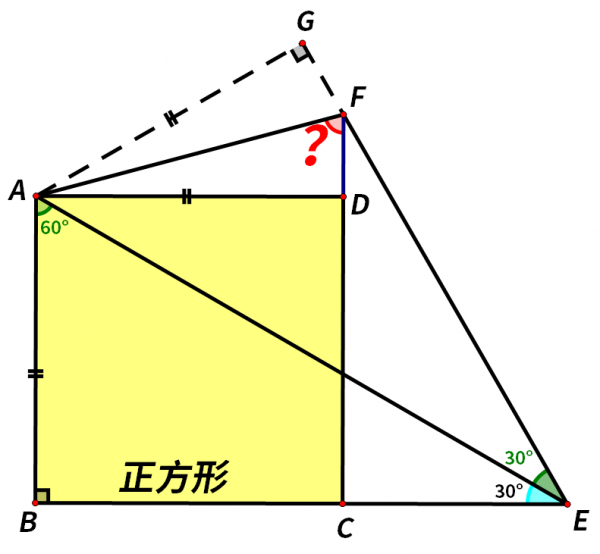
我們可以延長EF,過點A作EF延長線的垂線。如圖,AG⊥EG。
四邊形ABCD為正方形,∠B=90°。
根據角平分線的性質,角平分線上的點到角兩邊的距離相等,可得AB=AG。
而由四邊形ABCD為正方形,可得AB=AD,
等量代換,AG=AD。
在直角三角形AFD和直角三角形AFG中,
AF=AF(公共邊),AD=AG,
由HL證全等的方法,可得直角三角形AFD和直角三角形AFG全等,
所以∠AFD=∠AFG,
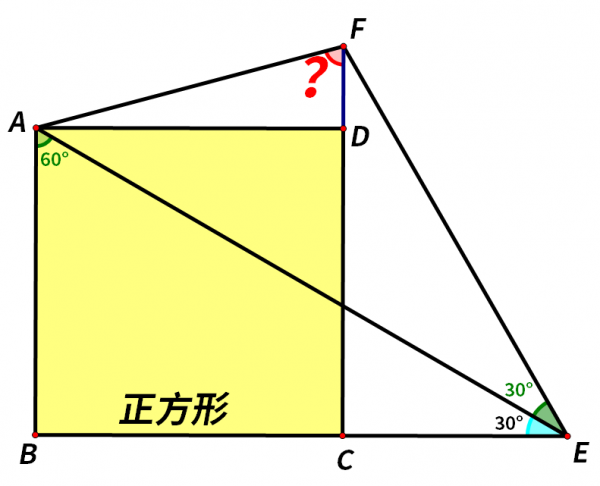
而∠CFE=180°-∠ECF-∠CEF=180°-90°-60°=30°,
所以∠AFD=(180°-∠CFE)÷2=(180°-30°)÷2=75°。