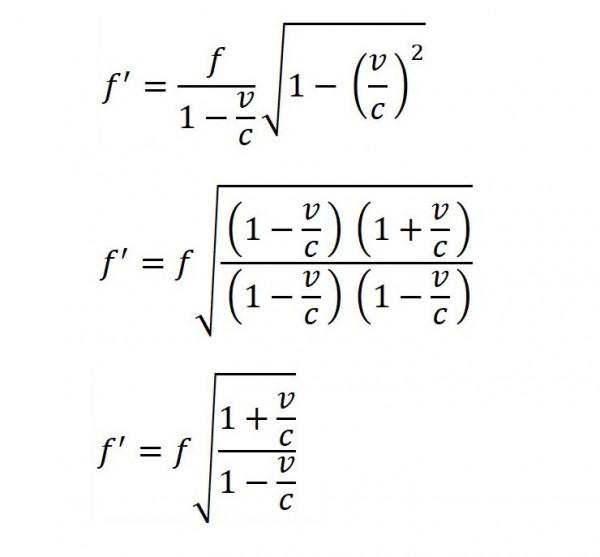你真的瞭解多普勒效應嗎?
別太自信,先來看一個小測試:
動靜等觀?太天真了!
沒錯,聲源運動和觀測者運動完全是兩回事!
本文較為硬核,請酌情跳過部分內容。
很多人只是籠統地知道多普勒效應是聲源或觀測者運動時觀測到的頻率變化,很多科普作品、教科書也只提供這種籠統的介紹。
這就讓很多人(包括曾經的我)錯過了太多太多精彩的物理,就多普勒效應而言,這暗含著關於絕對空間和相對空間的思考。
想要真正理解這一切,就需要了解一些聲波的數學表達。想要描述頻率的變化,就要先描述頻率本身。
這並不複雜,只涉及到加減乘除、平方、開方,以及一些想象力。
聲源完成一次振動需要的時間就是聲波的週期,聲源在單位時間內振動的次數就是聲波的頻率。
週期和頻率是一一對應的,選擇合適的頻率就能讓週期和頻率滿足一個非常簡單的關係:
聲波在介質中傳播的速度就是波速,經過一個週期,聲波傳播的距離就是波長,所以它們三者之間滿足這樣的關係:
而多普勒效應的精髓是:
所有關於多普勒效應的討論都是對這個公式的各種變形。
(1)如果聲源和觀測者都靜止,那麼觀測者測到的聲波頻率就是:
在這裡已經需要我們思考一下“絕對空間”了,是否存在一個“絕對空間”,讓我們可以定義絕對的靜止和絕對的運動?
對於聲波,答案是:可以!
聲波的傳播需要介質,而聲波的介質(比如空氣)可以構成一個區域性的“絕對空間”。
相對於聲波的介質靜止,就是“絕對的靜止”,相對於聲波的介質運動,就是“絕對的運動”。
此時,你只需要知道本文討論聲波時提到的靜止都是相對於聲波的介質靜止,然後向下閱讀。
(2)如果聲源向觀測者運動,觀測者靜止,那麼觀測者測到的波長就會變化。
為了理解波長的變化,可以認為每經過一個週期,聲源就發出一個波面(通常是球面),波面之間的距離就是波長。
從聲源發出一個波面開始計時,經過一個週期,已經發出的波面向前傳播了一個距離,但是聲源也向前運動了一個距離,與此同時發出了一個新的波面。
這就讓兩個波面之間的距離變短了,也就是波長變短了。
這就是對波長變化的定量描述,而聲速是不隨聲源運動而變化的(切記),所以觀測者測到的聲波頻率是:
(3)如果聲源靜止,觀測者向聲源運動,那麼觀測者測到的聲速就會變化。
如果你是一個善於獨立思考的人,你可能會問:
以觀測者為參考系,聲源是運動的。上面剛剛說了“聲速是不隨聲源運動而變化的”,這裡的聲速怎麼就變化了?這不是聲源運動導致的聲速變化嗎?
注意,以觀測者為參考系,聲波的介質是運動的。是聲波介質的運動導致的聲速變化,而不是聲源運動導致的聲速變化!
(聲波的介質構成的“絕對空間”相對於觀測者運動了。)
聲速的變化很容易描述,只要讓原本的聲速加上聲波介質和觀測者的相對速度就行了。
這就是對聲速變化的定量描述,而波長是不隨觀測者運動而變化的,所以觀測者測到的聲波頻率是:
如果你理清了上面提到的兩種多普勒效應,那麼就可以回到開頭的那個小測試了:
這就是定量描述的力量!
我相信此時的你可以更好地理解這句話:
相對於聲波的介質靜止,就是“絕對的靜止”,相對於聲波的介質運動,就是“絕對的運動”。
(4)如果聲源向觀測者運動,觀測者也向聲源運動,那麼觀測者測到的波長和聲速就會變化。
我相信你可以依葫蘆畫瓢,得到下面的公式:
這就是描述聲波多普勒效應的“統一公式”,如果聲源遠離觀測者,或者觀測者遠離聲源,只需要把上面公式裡的聲源速度或觀測者速度取成負值就可以了。
上面的討論說明了絕對空間的存在嗎?
沒有,聲波的介質終究只是和絕對空間類似,終究不是絕對空間。
來自狹義相對論的修正
看到“狹義相對論”這五個字,不要恐慌,這個修正非常簡單。
按照經典的時空觀(絕對的時間),波源和觀測者之間的距離隨時間變化的時候才會讓觀測者測到的頻率發生變化,產生多普勒效應。
如果波源繞著觀測者做圓周運動,或者觀測者繞著波源做圓周運動,它們的距離不會變化,也就不會有多普勒效應。
但是,按照狹義相對論的時空觀(相對的時間),事實並非如此。
如果在相對於觀測者A運動的物體上發生了一個事件,碰巧在運動的物體上也有一個觀測者B,那麼觀測者A和觀測者B測到的這個事件經歷的時間是不同的。
觀測者A認為這個事件經歷的時間更長,這就是所謂的“時間膨脹”,這個公式是洛倫茲變換的一個推論。
(關於洛倫茲變換,各位讀者可以參考筆者之前的作品,評論區裡會附上鍊接。)
把這個結論用到波源繞著觀測者做圓周運動的情景中(觀測者繞著波源做圓周運動的情景也一樣),觀測者會發現聲源振動的週期變長了,這就使其測到的聲波頻率也變小了。
這就是“橫向多普勒效應”,是時空本身的屬性,這種頻率變化只與聲源和觀測者的相對運動速度的大小有關,與它們相對運動速度的方向是沒有關係的。
之前討論的一大堆波源和觀測者之間的距離隨時間變化的情景也可以被稱為“縱向多普勒效應”。
沒錯,發生“縱向多普勒效應”的時候也會摻雜著“橫向多普勒效應”(時間膨脹),你可能已經猜到了修正“縱向多普勒效應”公式的方法:
這就是修正後的描述聲波多普勒效應的“統一公式”,聲波的各種多普勒效應都可以由這個公式統一地描述!
光波,這才是動靜等觀!
提及多普勒效應,肯定繞不開光波的多普勒效應。提及絕對空間與相對空間,更是繞不開光波的多普勒效應。
知道了描述聲波多普勒效應的公式,描述光波的多普勒效應就已經不是什麼難事了。
我們只需要知道“光速不變”,不管是光源運動還是觀測者運動,觀測者測到的光速都不變。也就是說,光波的多普勒效應只由波長的變化引起。
那麼,這裡的運動是相對於誰運動?可以類比聲波,認為是相對於光波的介質靜止嗎?
你可能已經發現了“光速不變”讓光源運動與觀測者運動變得“不可區分”了。不管是哪一方運動,描述光波多普勒效應的公式都是一樣的。
我相信你可以完成下面的操作:
沒錯,這就是描述光波多普勒效應的“統一公式”,光波的各種多普勒效應都可以由這個公式統一地描述!
如果光源和觀測者相互遠離,只需要把上面公式裡的光源速度或觀測者速度取成負值就可以了。
有些人還搞了一些操作,把公式變了個形式:
利用這個形式的公式可以發現光波比聲波簡單多了,光波的多普勒效應不用區分(也無法區分)到底是光源運動還是觀測者運動!
這就意味著,我們無法定義絕對的靜止和絕對的運動。光波與聲波不同,光波的介質不會構成一個區域性的絕對空間,甚至於,光波壓根就沒有對應的介質!
正文基本結束,還有一件筆者藏在心裡很久的事,要在這裡說一下:
有一種特殊情況是光源或觀測者徑直地向對方靠近,這種情況的公式更簡單:
不過很多資料都喜歡把這種情況的公式寫得“面目全非”:
(之所以說它“面目全非”,是因為這種形式的公式無法直觀地體現物理意義。)
筆者不知道各種資料為什麼非要把光波多普勒效應的公式寫得“面目全非”,好像生怕讀者知道這些公式的聯絡一樣,也好像生怕讀者真正學到一些物理一樣。