機器之心報道
機器之心編輯部
頂尖數學家表示:「這是利用機器學習做出的第一個重大數學發現。」
多年來,數學家們一直使用計算機來生成資料以幫助搜尋數學模式,這種被稱為實驗數學的研究方法產生出許多重要的猜想,例如BSD猜想。雖然這種方法已經取得成功並且相當普遍,但從這些資料中識別和發現數學模式仍然主要依賴於數學家。
隨著計算機領域的飛速發展,利用計算機尋找數學模式變得越來越重要,因為計算機生成的資料量爆炸式激增。一些非常複雜的數學物件(例如具有數千個維度的物件),可能因為太深奧而無法直接推理。出於這些限制,DeepMind的研究者希望採用人工智慧以全新的方式增強數學家的洞察力。
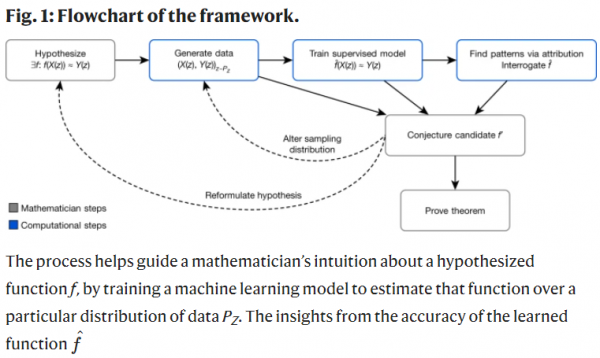
數學家的直覺在數學發現中扮演著極其重要的角色,只有結合嚴格的形式主義和良好的直覺才能解決複雜的數學問題。下圖的框架描述了一種通用方法,數學家可以透過該方法使用機器學習工具來啟發他們對複雜數學物件的直覺。這是一種自然且富有成效的方式,將統計學和機器學習很好地融入了數學研究。
從概念上講,這個框架提供了一個直覺試驗檯,可以快速驗證兩個量之間的關係直覺是否值得研究,如果是,試驗檯會指導它們之間如何相關。DeepMind已經使用上述框架幫助數學家在兩種情況下獲得有影響力的數學結果。
DeepMind作為一家全球領先的人工智慧公司,他們探索了機器學習 (ML) 在識別數學結構和模式方面的潛力。現在他們幫助數學家解決了一些數學難題,成為AI首次探索純數學的前沿研究,相關論文今天已在《自然》雜誌上發表。
論文地址:https://www.nature.com/articles/s41586-021-04086-x
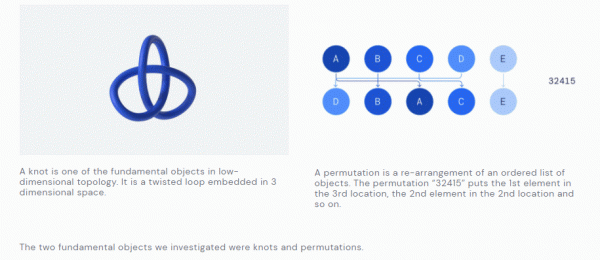
具體來說,DeepMind與頂級數學家合作,將AI應用於純數學中的兩個領域:拓撲和表示論。其中DeepMind與牛津大學的 Marc Lackenby 教授和András Juhász 教授一起,透過研究紐結 (Knot)的結構發現了不同數學領域之間的意外聯絡;與悉尼大學的 Geordie Williamson 教授一起,DeepMind發現了一個關於排列猜想的新公式,該猜想幾十年來一直未解決。
拓撲難題
DeepMind與牛津大學的 Marc Lackenby 教授和András Juhász教授一起,透過研究紐結 (Knot)的結構發現了不同數學領域之間的意外聯絡。
低維拓撲是數學中一個活躍且有影響力的領域,DeepMind發現了紐結代數和幾何不變數之間的關係,建立了數學中一個全新的定理。這些不變數有許多不同的推導方式,但DeepMind主要關注兩大類:雙曲不變數和代數不變數。這兩種型別的不變數來自不同的數學學科,因此在它們之間建立聯絡是非常有趣的。
下圖顯示了紐結不變數的一些例子。
DeepMind假設在一個紐結的雙曲不變數和代數不變數之間存在一種未被發現的關係。監督學習模型能夠檢測大量幾何不變數和signature σ(K) 之間存在的模式,並用歸因技術(attribution technique)確定最相關的特徵。下圖(a) 顯示了cusp幾何的三個不變數,圖 3b 中部分地顯示了其中的關係。
表示論難題
在澳大利亞數學家、悉尼大學教授Geordie Williamson的幫助下,DeepMind藉助人工智慧解決了表示論中一個長期存在的猜想——組合不變性猜想。
Geordie Williamson
組合不變性猜想指出某些有向圖和多項式之間應該存在關係。DeepMind使用機器學習方法確認了這種關係確實存在,並確定其可能與稱為破碎的二面角區間(broken dihedral interval)和外反射(extremal reflection)的結構有關。有了這些知識,Williamson教授就能夠發現一個令人驚訝的演算法來解決組合不變性猜想。
表示論是數學中抽象代數的一支。旨在將代數結構中的元素「表示」成向量空間上的線性變換,藉以以研究結構的性質。其中,任何表示都是不可約表示的直和。不可約表示的結構由 Kazhdan-Lusztig (KL) 多項式控制,這些多項式與組合學、代數幾何和奇點理論都有著深厚的聯絡。
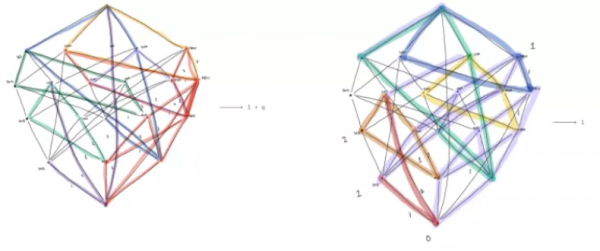
組合不變性猜想作為一個關於 KL 多項式的開放猜想,已經存在了約40年,但只有部分進展。在理解物件之間關係方面取得進展的一個障礙是 Bruhat 區間。下圖給出了小 Bruhat 區間及其 KL 多項式的例子。
DeepMind的研究把組合不變性猜想作為初始假設,利用機器學習的方法發現了一個能夠預測 KL 多項式Bruhat區間的監督學習模型,並且具有相當高的準確率。透過測試將 Bruhat 區間輸入網路的方式,研究者發現某些圖表和特徵的選擇特別有助於準確預測。特別地,藉助更準確的估計函式,研究者還發現有一種受先前工作啟發的子圖足以計算 KL 多項式。
該研究已經在超過 300 萬個示例中對新演算法進行了計算驗證,下圖是表示論歸因的例子。
研究者進一步探究了機器學習是否可以闡明不同數學物件之間的關係。下圖顯示了兩個「Bruhat 區間」及其相關的「Kazhdan-Lusztig 多項式」其中,Bruhat 區間是一個圖表,它代表了透過一次只交換兩個物件來反轉物件集合的順序的所有不同方式。KL 多項式能夠告訴數學家一些關於該圖在高維空間中存在的不同方式的資訊。當 Bruhat 區間有 100 或 1000 個頂點時,有趣的結構才開始出現。
毫無疑問,機器學習和人工智慧系統為識別和發現數學模式提供了廣闊的前景。DeepMind表示他們希望這項研究成為將人工智慧作為純數學中有用工具的開始。我們相信,那些懸而未決的數學難題,一定會透過數學家與AI的合作突破,人類的直覺也會藉助AI上升到一個新的水平。
參考文獻:https://deepmind.com/blog/article/exploring-the-beauty-of-pure-mathematics-in-novel-ways