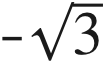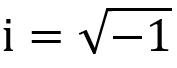數學的目的是並不是證明幾個孤立結論,而是探索未知的邏輯關係。就這層意義上說,Langlands 綱領或許是近幾十年來最重要的數學成果——即便它只是一些未經證實的猜想。
Langlands 綱領源於 1967 年加拿大裔美國數學家 Robert Langlands 寫給著名法國數學家 André Weil 的一封信,在這封信中,他建立了表示論/自守形式與代數數論中 Galois 群的聯絡。如今,由此生出的數學理論已經涉及到數學的方方面面,甚至有幾何 Langlands 綱領涉及物理學中的規範場論。讓我們跟隨女數學家 Ana Caraiani 的腳步,一窺數學的大一統理論。
Ana Caraiani,站在帝國理工學院附近的Serpentine橋上,從事數學研究,為該領域裡遙遠的分支架起橋樑。圖片來源:Philipp Ammon/Quanta Magazine
採訪者 | Steve Nadis
受訪人 | Ana Caraiani(帝國理工學院教授)
翻譯 | 張和持
Ana Caraiani 在普林斯頓大學的本科畢業論文由安德魯·懷爾斯(Andrew Wiles) 指導。懷爾斯是一位著名數學家,1994年,就是他證明了 費馬大定理。這位名聲在外的學者交給學生的問題自然困難重重,而 Caraiani 並沒有她導師當年的運氣。不過,雖然並沒有取得顯著的進展,她也不曾氣餒。
Caraiani說,"這個題目的重點不一定是解決這個問題。我認為懷爾斯在教我,不應該把所有的時間都花在你知道如何做的事情上。那些真正困難的問題值得花時間去解決,只是可能真的太難了。”
在做畢業論文的過程中,她學到了很多數學研究的方法。“你不可能總是按部就班地做數學。如果你卡在了問題的某個部分,就先別管它,去做其他部分。” Caraiani後來進行了非常廣泛的合作研究,目的是將數學的各個不同領域聯絡在一起,而做畢業論文的經驗讓她受益匪淺。她所從事的研究被稱為 Langlands 綱領,由加拿大數學家Robert Langlands於上世紀 60 年代建立。這是當今數學界最為龐大,最富野心,同時也是最具挑戰性的任務。
Caraiani 現在擔任倫敦帝國理工學院教授,同時獲得了皇家學會大學研究獎學金(URF)。她從來都不迴避任何挑戰。在羅馬尼亞首都布加勒斯特長大的她,經常會遭遇與她自身能力無關的挫折。2001年,作為一名高中生,她成為數十年來第一個有資格參加國際數學奧林匹克競賽(IMO)的羅馬尼亞女性,並在當年摘得一枚銀牌,此後兩年又連續摘得金牌。不過儘管獲得瞭如此成功,她仍然感覺自己是不受歡迎的,也很少得到鼓勵。
“有些人,包括舉辦大賽數學老師們,都讓我不要抱太大期望,”她說。“而我想要證明他們都錯了。”
Caraiani 對Quanta雜誌講述了她追求數學的經歷以及研究 Langlands 綱領的工作,而後者可以理解為“通向數學大一統理論之路”。為了讓文章更加清晰,我們對採訪內容進行了壓縮與編輯。
Caraiani 致力於當今最雄心勃勃的數學專案之一,即Langlands計劃。這是一項高度協作的努力,她經常與帝國理工學院的同事在Dalby Court會面。圖片來源:Philipp Ammon/Quanta Magazine
你闖進男性主導的 IMO 之後,情況有沒有發生轉變?
當時我在高中從來不被人看好,而如今學校的女生會得到很多鼓勵。不過即便如此,我還是看到自己身邊的人遭受隱晦的歧視。如果別人都視你為異類,那麼要開展研究或是建立長期合作關係就會困難重重。而且你很難被認真對待,每次都必須得證明自己的能力。
我意識到,其實相比大多數同行,我一直很幸運,現在也已是小有名氣。不過我還是覺得,數學界並不像它應有的那麼包容——不僅僅是對於女性,對其他弱勢群體也是一樣的。在我研究的領域中更是這樣,Langlands 綱領的研究需要大量專業知識,就連入門也存在巨大的障礙。
我只能儘自己所能幫助他人,一起探索這一驚人的領域,不過我覺得還是不夠。我努力為女性,以及其他弱勢群體提供生存空間,爭取會議席位,讓她們參加我的研究小組。我很高興自己的研究小組中女性佔比高於平均水平。
是什麼吸引你來到這個驚人領域的?
我2007年從普林斯頓大學畢業,那時懷爾斯鼓勵我去哈佛大學深造,那樣我可以跟 Richard Taylor學習——他對費馬大定理的證明做出了關鍵貢獻。而我之所以做 Langlands 綱領正是隨的他。
不過對於我來說,還有更深層次的吸引力。Langlands 綱領是要旨,從本質上說是給數學的不同分支建立聯絡。而我喜歡數學的所有分支——數論、分析、幾何、拓撲等——如果我做 Langlands 綱領的話,就不必將自己的研究限制在任何分支中。如果我們遇到還不會證的猜想,就可以嘗試聯絡其他數學分支,用其他相關工具,就有可能取得進展。
在你的事業中,所謂“進展”是什麼意思呢?
我和同事們所做的工作,就是在不同數學分支間搭起橋樑——具體來說,橋的一邊是Galois 群與Galois表示,另一邊是模形式與其推廣。
我們從Galois群說起。比方說 x2-3=0這個多項式方程,它的解,或者說根,是
和
。顯然,這兩個數字是關於y軸對稱的。所謂Galois群並不是多項式方程根的群,而是根的對稱群。
而如果考慮次數為5的多項式(次數指最高次項次數,比如x5或y5),這時方程就變得非常複雜,其 Galois 群也變得複雜。Galois表示可以用來簡化問題,這時我們就不必研究整個Galois群,只需要觀察它的某些部分,或者說截面。就像是取3維物體的2維截面一樣;雖然截面並不包含所有原始資訊,但很多時候也夠用了。
那橋的另一邊呢?
模形式是一種高度對稱,定義在上半複平面上的函式,其中我們用x軸代表實數,y軸代表虛數(也就是
的倍數)。我們只考慮性質“良好”或者說光滑的函式,也就是指函式不會跳躍,也沒有尖突。也可以說函式是可導的。
我們可以把上半複平面分成小區域,或者說“瓦片”。而由於對稱性,我們只需要知道其中一個瓦片上的函式值,就可以知道所有值。接著,我們可以取無窮多個瓦片,並把相鄰的粘在一起,這樣就產生了一個曲面,我們稱為模曲線。
即便這些都是完全不同的概念,也能透過 Langlands 綱領來說明他們的等價性?
沒錯,連線模形式(屬於分析)與Galois 表示(屬於數論與算數幾何)的橋樑,最初建立於上世紀 70 年代,從那時開始,研究人員就一直在加固這座橋。
在Langlands對應中,我覺得最神奇的莫過於:你可以用完全不同的方法,分別在模形式和Galois兩邊得到同樣一串數字。你要做的,基本上就是把模形式——也就是那些高度對稱的函式——分解為正弦函式和餘弦函式。這樣你就能得到三角函式的係數。而對於Galois這邊,你只需要數一下多項式方程的根的個數。
能在實際計算中觀察到這種現象,即便對我來說,也非常震驚。因為要真正建立這樣的聯絡,得用到比這多得多的數學物件。
“我和同事們所做的工作,就是在不同數學分支間搭起橋樑。”圖片來源:Philipp Ammon/Quanta Magazine
來回的兩個方向需要不同的橋嗎?
的確是這樣。第一座橋是單向通道。如果你想從 Galois表示這邊開始,往模形式那邊走,就可以使用Taylor-Wiles方法,這個方法最早是用來證明費馬大定理的。現在我們已經能雙向行走了。
為什麼要這樣大費周章?透過這些橋樑還能讓你們做些什麼?
建立這些關係,展示不同數學之間的共同點,能帶來智力方面的滿足。當然,它也是有實用價值的。對於某些數學問題來說,在橋的一邊會比另外一邊更容易解決。面對一個很難的數學問題,我們經常需要在其中一邊做一些研究,然後再到另一邊做更多工作。為了證明某些命題,你可能需要來回過橋,這樣你就必須得能在兩個方向上自由穿行。
在這個領域中,一個重要的目標是要在更一般的條件下造橋。這樣我們就能讓Langlands 綱領的研究範圍不斷擴張。
在造橋過程中,你做出了什麼貢獻呢?
數學家們已經意識到Taylor-Wiles方法對侷限性:它針對2維情況效果良好,但在3維就失效了。2012年,Frank Calegari和David Geraghty想到了一個改進方法,以適用 3 維情況。然而他們表示,要讓這個方法起作用,首先得解決他們提出的三個猜想。
我的同事Peter Scholze在2013年解決了第一個猜想;這個猜想建立了第一座橋——從模形式到Galois,這座橋遠比原來的2維情況要寬的多,這樣才能與3維情況下出現的新現象相容。
在2015年年底,Sholze 和我意識到,我們最近的工作可以用來解決第二個猜想,要是這個猜想得到證實,就能精確控制這座橋著陸的位置。雖然這個方法失敗了,但是我們又想出了很有希望的新方法。這時,Taylor建議我們在普林斯頓高等研究院(IAS)組織一場研討會來完善我們的工作,想辦法解決第二個猜想。
雖然Caraiani不認為Langlands綱領最終能解釋數學中的一切,但她覺得有一天它可能會連線起數學的所有領域丨圖片來源:Philipp Ammon/Quanta Magazine
為什麼要跟讓別人來參與這項工作,而不是自己解決第二個猜想?
整個證明過程從幾何跨越到數論。Sholze 和我做的是幾何部分,但我們認為自己並不是數論方面最好的人選。我們覺得尋求合作能讓專案進展得更快。
結果如何呢?
我們已經解決了第二個猜想這個目標,並且找到了一個方法來繞過第三個猜想。我們建起了反方向的橋——由Galois到模形式的3維情況。這讓我們成功越過了Taylor-Wiles方法失效的障礙。而且這座橋不單單是對3維,對任意維也是有效的。論文已經在 2018 年聖誕節那天掛到網上,現在正在接受期刊的審校。
現在你又在做什麼研究呢?
我們對Calegari和Geraghty的第二個猜想,只在兩種特殊情況下做出了證明。現在我正在與之前 10 位合著者之一的James Newton合作,想辦法在最一般的條件下證明這個猜想。
我還是對第三個猜想很感興趣,即便我們之前繞過了它。它預測了志村簇(Shimura varieties)的某些性質,而我對此興趣濃厚,希望今後能對它有更深的瞭解。
另外,還存在某些情況,我們對於如何造橋一無所知。在我們的領域中一個重大的目標就是在儘可能一般的條件下造橋,比如使用任意數繫上的多項式。這樣我們就能擴充套件 Langlands 綱領的研究範圍。
這種統一最終能走多遠?
我並不認為Langlands理論有一天能解釋所有數學,不過我還是認為,它起碼能觸及數學的所有方面。
Robert Langlands的確高瞻遠矚。他在幾十年前建立了一整個網路的猜想,而這個領域的範圍也逐步擴大。我們跨過的橋越多,能提出的新猜想,能前往的新目的地也更多。似乎這些取得的進展,都是為了讓我們看到前方更為廣闊的天地。我並不認為任何人會期待這個綱領走向終結。
本文譯自 The Mathematician Who Delights in Building Bridges,原文連結:https://www.quantamagazine.org/ana-caraiani-delights-in-building-mathematical-bridges-20211117/