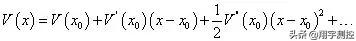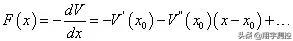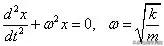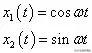來源:豆瓣使用者醬拌油潑蛋
簡諧振動是最普遍的運動形式之一。彈簧振子、單擺等絕大多數振動,在振幅不太大時都符合簡諧振動的形式。固體中原子在平衡位置附近的振動,也用簡諧振動來描述。甚至量子場論中的基本粒子,也用一系列簡諧振動形式的“場”來描述。
質點的運動,如果被勢場束縛在一個有限的區域內,則稱為束縛態運動;反之,如果能到達無窮遠處並保持大於零的動能,則稱為散射態運動。以無窮遠處為勢能零點,散射態的動能大於勢能,總機械能為正;而束縛態的動能小於勢能,總機械能為負。最簡單的運動形式是,當勢場不存在時,質點將做勻速直線運動,這種情形稱為自由粒子。除去自由粒子外,最簡單、最普遍的一種運動形式就是簡諧振動了。
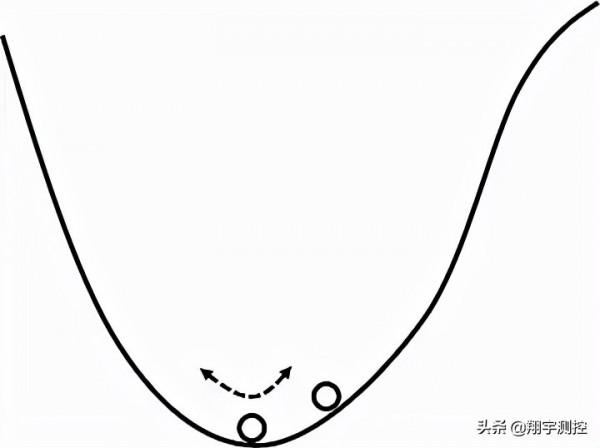
簡諧振動是一種束縛態運動形式,質點在平衡位置附近一個有限的範圍內運動(如下圖所示)。一維勢場中的束縛態運動通常是週期性的,當質點回到初始位置、方向相同時,完成一個運動週期,此後將重複這個週期。一般的一維束縛態運動,週期是與振幅有關的。簡諧振動是一種特殊情形:勢場是二次函式形式時,週期與運動振幅無關。
在平衡位置附近足夠小的範圍內,一般形式的勢能都可以近似為二次函式形式。將勢能按平衡位置附近的位移做級數展開:
平衡位置附近的勢能:
其中,第一項是常數項不產生作用;第二項是線性項,平衡位置為勢能的極小值點,故此項為0;主導項為第三項,即二次項。從受力分析的角度:
平衡位置附近的受力:
平衡位置處外力為0,因此第一項消去;主導項為第二項,即線性回覆力。
因此,一般的束縛態振動在振幅較小時,都可以近似為簡諧振動。簡諧振動的勢能是位移的二次函式,所受外力正比於位移,指向平衡位置方向。通常把簡諧運動的勢能和回覆力寫作:
根據牛頓第二定律、拉格朗日方程或哈密頓方程,可得到簡諧運動的位移滿足的運動方程:
這是一個非常著名的二階線性常係數微分方程,它有兩個線性無關的通解:
它們是以ω 為角頻率的週期性運動,也可以看作勻速圓周運動在一個方向上的投影。將這兩個通解做線性疊加,得到一般解:
其中,A 稱作運動的振幅,與運動的總機械能大小有關;φ 稱作運動的相位。振幅與相位由運動的初始狀態決定,而頻率只由勢能本身決定。
簡諧運動的位移、速度、加速度(外力)都以相同的頻率隨時間振盪變化。這種振動在介質中傳播,可以形成機械波;電場和磁場按這種振盪方式隨時間變化,可以形成電磁波;在量子力學中,簡諧振子因具有優良的數學和物理性質,被作為描述粒子的最常用模型。
北京神州翔宇技術有限公司